Från Rilpedia

Inom mängdteorin används Alef-tal för att ange kardinaliteten, d.v.s. antalet element i oändliga mängder. Alef är namnet på den första bokstaven i det hebreiska alfabetet, 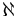. Det finns oändligt många Alef-tal och de betecknas 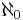, , 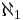o.s.v.:

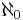(uttalas alef-noll) är kardinaltalet för alla uppräkneligt oändliga mängder. Exempel på sådana mängder är de naturliga talen och heltalen.

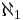(uttalas alef-ett) är kardinaltalet för mängden av alla uppräkneligt oändliga ordinaltal. Enligt den s.k. kontinuumhypotesen är detta kardinaltal lika med kardinaltalet för mängden av alla reella tal, 2^Alef-0. D.v.s. .

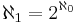är kardinaltalet för mängden av alla ordinaltal av kardinalitet Alef-1.

Efter talen 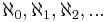följer 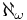som är ett singuljärt kardinaltal.

Mängden av reella tal är alltså inte av storleken Alef-0, utan större. Denna mängd säges därför istället vara ett kontinuum, "har kontinuums mäktighet". Av Cantors sats följer att det finns ingen gräns på hur stora oändligheter vi kan bilda.

Om man låter P(A) beteckna potensmängden av mängden X gäller t.ex: X<P(X)<P(P(X))<..., även för oändliga mängder X.

Se även

• Uppräknelig
• Uppräkneligt oändlig
• Kontinuum
• Kontinuumhypotesen