Från Rilpedia

Cantors sats (efter Georg Cantor) är en sats inom mängdteorin som innebär att det inte finns någon gräns för hur stora kardinaltal man kan bilda: Om man bildar potensmängden av en mängd (ändlig eller oändlig), så får man alltid en ännu större mängd. Att potensmängden till en mängd alltid är en mängd är innebörden i potensmängdsaxiomet.

Satsen lyder: α < 2^α för alla kardinaltal α

Bevis

Att potensmängden har större kardinalitet innebär att det inte finns någon bijektion 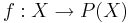. Vi kommer visa detta genom ett motsägelsebevis.

Antag att det finns en sådan avbildning f. Studera ett element i bildmängden: 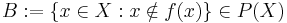.B är väldefinierad, eftersom f är väldefinierad. Eftersom f är bijektiv finns ett 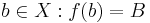. Vi ställer oss frågan ?

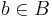Antag 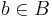. Detta stämmer inte, ty B = f(b) och kravet för att vara med i B är just 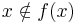, så .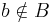

Antag 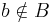. Detta kan inte heller stämma, ty B = f(b), så b uppfyller kravet för att vara med i B, så .

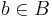Motsägelse! Vårt ursprungliga antagande att det finns en sådan avbildning f måste därför förkastas, och satsen är bevisad.

B är ett exempel på en barberarmängd.

En annan formulering av samma sak är |α| < |P(α)| för alla mängder α. Här står P(α) för potensmängden av α (dvs mängden av alla delmängder till α) och |α| betyder kardinaliteten för α (dvs antalet element i α). Ett annat sätt att formulera satsen i ord är att säga att varje mängd har fler delmängder än den har element.

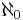är kardinaliteten för de naturliga talen, den minsta oändliga mängden. Enligt Cantors sats är 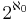alltså en större oändlighet. 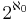är kardinaliteten för de reella talen. Enligt kontinuumhypotesen är 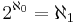, dvs 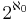är den kardinalitet som följer närmast efter 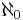i storleksordning. I vanlig mängdteori, ZFC, kan man dock inte bevisa att kontinuumhypotesen är vare sig sann eller falsk, det är ett s k oavgörbart påstående.