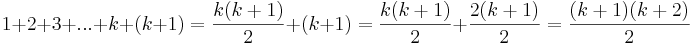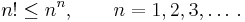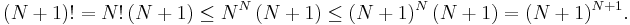Induktion (matematik)
Från Rilpedia
Induktion, eller fullständig matematisk induktion som den också kallas, är en matematisk teknik för att bevisa påståenden som på något sätt har med de positiva heltalen att göra. Tekniken kan även tillämpas på de matematiska objekt som är vidareutvecklingar av de positiva heltalen: Ordinaltalen.
Tekniken kan förstås med en analogi: Du har lika många dominobrickor som det finns positiva heltal och på varje dominobricka är skrivet ett positivt heltal. (Det finns inte två brickor på vilka samma heltal är skrivet.) Du ställer upp dominobrickorna på högkant i den ordning som talen på dem föreskriver, så att när en bricka välter så knuffar den till nästföljande bricka så att även den välter. Induktionsprincipen säger att samtliga dominobrickor kommer att bli välta, när väl den första brickan har blivit vält.
Innehåll |
Induktionsprincipen: Formell beskrivning
Låt P(n) vara ett påstående som har att göra med ett positivt heltal n, och antag att följande påståenden är sanna:
- P(1) är sant.
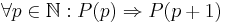 .
.
Då är påståendet P(n) sant för varje val av det positiva heltalet n.
Principen för matematisk induktion
- Låt A vara en mängd av positiva heltal som innehåller talet ett. Om A innehåller talet n+1 då det även innehåller talet n, så är A lika med mängden av alla positiva heltal.
Denna formulering kan man bevisa på ett elegant sätt med hjälp av välordningsaxiomet för de positiva heltalen.
Bevis av principen för matematisk induktion
Vi skall använda en matematisk teknik som kallas motsägelsebevis. (Latin: Reductio ad absurdum.) Tekniken går ut på att anta att motsatsen till det vi vill bevisa är sann, och visa att detta leder fram till en motsägelse; ett påstående som aldrig kan vara sant.
Beteckna med symbolen A en mängd som innehåller talet ett och som även innehåller talet n+1 om det innehåller det positiva heltalet n. Vi vill visa att mängden A är lika med mängden av alla positiva heltal.
- Antag att A inte är lika med mängden av alla positiva heltal.
Då finns det positiva heltal som ligger utanför mängden A. Samla ihop dessa till en mängd som vi betecknar med symbolen B; detta är en icke-tom mängd bestående av positiva heltal. Enligt välordningsaxiomet för de positiva heltalen innehåller B ett minsta element, som vi betecknar med symbolen m.
Eftersom mängden A innehåller talet ett, kan elementet m inte vara talet ett; det är därför större än talet ett. Då är elementet m-1 ett positivt heltal som är mindre än talet m. Talet m-1 kan inte ligga i mängden B, eftersom m-1 då vore det minsta elementet i B. Därför måste talet m-1 ligga i mängden A. Men om elementet m-1 ligger i mängden A, så ligger det efterföljande talet (m-1) + 1 också i mängden A, det vill säga att talet m ligger i mängden A.
Vi har härmed visat att det finns ett element (m) som både ligger innanför och utanför mängden A, vilket är ën motsägelse.
- Det var därför fel av oss att anta att mängden A inte var lika med mängden av positiva heltal.
Härmed är principen om matematisk induktion bevisad.
Exempel
Nedan följer några exempel där man kan använda principen om matematisk induktion för att bevisa olika påståenden om positiva heltal.
Aritmetisk talföljd
- Sats att bevisa:
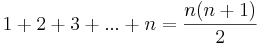 , där n är ett naturligt tal.
, där n är ett naturligt tal.
Visa först att det gäller för ett basfall n=1, vänsterledet är ju givetvis 1. För högerledet får vi att:
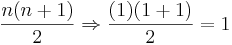 då n=1. Därmed har vi visat att satsen gäller för n=1.
då n=1. Därmed har vi visat att satsen gäller för n=1.
Om vi nu antar att satsen gäller för ett godtyckligt tal n=k, så återstår det att visa att detta medför att det även är sant för n = k + 1.
- Antagande:
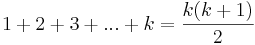
För n = k + 1 gäller då att visa att: 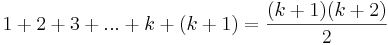
I vänsterledet är termerna upp till k vårt antagande, som vi nu drar nytta av:
Eftersom vi har visat att satsen gäller för n=1, och om det är sant för n=k så är det även sant för n=k+1, så säger induktionsprincipen att satsen är sann för alla naturliga tal 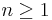 .
.
Tal på formen 32n + 1 + 52n är delbara med 4, men inte med 8
Man kan också göra tvärtom för att visa att om ett påstående är falskt för n=p, så är det även falskt för n=p+1. Detta används i följande bevis.
- Bevisa att för varje naturligt tal n är talet 32n + 1 + 52n delbart med 4, men inte med 8.
Bevis: Förenkling ger k = 32n + 1 + 52n = 3 * 32n + 52n = 3 * 9n + 25n
För n=0 gäller alltså att k0 = 3 + 1 = 4, och för n=1 fås att k1 = 3 * 9 + 25 = 52. Både 4 och 52 är delbara med 4, men inte för 8. Nu har vi visat att det gäller för två basfall.
Antag nu att det är sant för n=p+1 (att det är delbart med 4), alltså kp + 1 = 27 * 9p + 25 * 25p, då gäller för n=p+2:
kp + 2 = 27 * 9p + 1 + 25 * 25p + 1
kp + 2 = 27 * 9p + 1 + 25 * 25p + 1 + 216 * 9p − 216 * 9p + 600 * 25p − 600 * 25p
kp + 2 = (27 * 9p + 25 * 25p) + 216 * 9p + 600 * 25p
Där parentesen motsvarar vårt antagande, som alltså skulle vara delbart med 4. 216 och 600 är båda delbara med 4, och således är även hela uttrycket delbart med 4. Induktionsprincipen ger att 32n + 1 + 52n är delbart med 4 för alla naturliga tal n.
Om vi antar att kp + 1 är delbart med 8, så visar det alltså sig att även kp + 2 är delbart med 8, eftersom 216 och 600 är det. Problemet här är att vi inte kan påbörja induktionen eftersom vi inte har något basfall. Om vi däremot hade antagit att det var falskt för kp + 1, hade vi funnit med samma metod som ovan att det även är falskt för kp + 2. Då det är falskt för basfallen n=0 och n=1 (att det är delbart med 8), säger induktionsprincipen att 32n + 1 + 52n inte är delbart med 8 för alla naturliga tal n, och det ursprungliga påståendet har bevisats.
Hur stort är talet n-fakultet?
För att få en uppfattning om storleken hos talen n-fakultet (n!) skall vi visa att:
För det första gäller olikheten då n=1, eftersom 1!=1. Vi antar att olikheten gäller för talet n=N och skall visa att den även gäller för nästa heltal, N+1.
Enligt principen för matematisk induktion gäller olikheten för alla positiva heltal, 1,2,3,... .