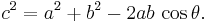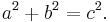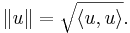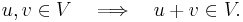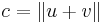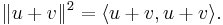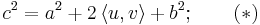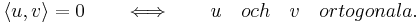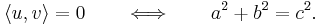Pythagoras sats

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Pythagoras sats anger sambandet mellan sidorna i en rätvinklig triangel. Den grekiske matematikern Pythagoras anses vara den första som bevisade satsen, men den var troligen känd av bland annat i Babylon sedan tidigare. Satsen är en av matematikens mest kända bland den breda allmänheten.

Den traditionella formuleringen av Pythagoras sats är:

Kvadraten på hypotenusan är lika med summan av kvadraterna på kateterna.

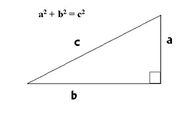
Hypotenusa är den längsta sidan i en rätvinklig triangel, som står mot den räta vinkeln och kateter är de två övriga sidorna, som bildar den räta vinkeln.

Innehåll

Alternativ formulering

Pythagoras sats
a2+b2=c2

Pythagoras kan med algebra uttryckas enligt följande:

Låt symbolerna a, b och c beteckna längderna hos de tre sidorna i en triangel, varav c är den längsta. Mellan längderna råder sambandet a2 + b2 = c2 om, och endast om, triangeln är rätvinklig.

Pythagoras sats kan även ses som ett specialfall av Cosinussatsen, som gäller för alla trianglar:

Låt symbolerna a, b och c beteckna längderna hos de tre sidorna i en triangel. Låt vidare symbolen θ beteckna vinkeln mellan triangelns två korta sidor, a och b. Följande samband råder mellan triangelns sidor och vinkeln mellan de två korta sidorna:
c^2 = a^2 + b^2 - 2ab \, \cos \theta.

Om triangeln i fråga är rätvinklig så är vinkeln θ lika med 90 grader, varför cosθ = 0. (För en beskrivning av beteckningen cos, se artikeln Trigonometrisk funktion.)

Egyptiska trianglar och pythagoreiska tripler

En så kallad egyptisk triangel är en rätvinklig triangel vars sidor har längder som förhåller sig till varandra som talen 3, 4 och 5: De två kateterna har längderna a = 3n och b = 4n och hypotenusan har längden 5n, där n är ett godtyckligt positivt heltal. Vi noterar att Pythagoras samband a2 + b2 = c2 gäller, eftersom talen 3, 4 och 5 är sidlängderna i en egyptisk triangel:

a2 + b2 = n2(32 + 42) = 25n2 = (5n)2 = c2.

Tre positiva heltal, a, b och c, utgör en pythagoreisk tripel, (a,b,c), om de uppfyller Pythagoras samband a2 + b2 = c2. Vi vet att sidlängderna i egyptiska trainglar utgör pythagoreiska tripler, men det finns även pythagoreiska tripler som inte är sidlängder i egyptiska trianglar. Följande är exempel på pythagoreiska tripler som ej är associerade med egyptiska trianglar: (5,12,13), (8,15,17) och (7,24,25).

Man kan bevisa att det finns lika många pythagoreiska tripler som det finns positiva heltal.

Bevis av Pythagoras sats

Det finns en bok av E.S. Loomis med den engelska titeln The Pythagorean Proposition som innehåller 367 olika bevis av Pythagoras sats.

Här presenteras ett av de mest eleganta geometriska bevisen.

Nedanstående bild visar en kvadrat, vars sida är a + b längdenheter lång. Genom att dela kvadraten i två olika pussel – på 'matematiska' säger man att kvadraten partitioneras på två olika sätt – kan man bevisa Pythagoras sats.

Pythagorean proof.png

Beviset består i att notera att de två pusslen båda innehåller samma blåa triangel, samma röda triangel, samma gröna triangel och samma gula triangel; De två små rosa kvadraterna i det vänstra pusslet måste då ha samma area tillsammans som den stora rosa kvadraten i det högra pusslet:

a^2 + b^2 = c^2.\,
Animation av ett geometriskt bevis.
Kvadrat med en mindre kvadrat inskriven

Generaliseringar av Pythagoras sats

Inom linjär algebra kan Pythagoras sats generaliseras till trianglar i inre produktrum av godtycklig dimensionalitet. Ett inre produktrum är ett vektorrum som besitter en inre produkt; en inre produkten mäter 'vinklar' mellan vektorrummets element. Ett inre produktrum är även ett normerat rum, vars norm är given av den inre produkten:

\Vert u \Vert = \sqrt{\langle u,u \rangle}.

Normen mäter 'längden' hos vektorrummets element.

Om u och v är två vektorer i ett inre produktrum, V, så är deras summa också ett element i samma rum:

u,v \in V \quad \Longrightarrow \quad u+v \in V.

Vektorerna u, v och u + v bildar tillsammans en 'triangel' i vektorrummet V; Triangelns 'längsta sida' är

c = \Vert u+v \Vert

och de två 'korta sidorna' är

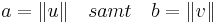a = \Vert u \Vert \quad samt \quad b = \Vert v \Vert.

Sambandet mellan normen och den inre produkten låter oss uttrycka normen av summan u + v på följande sätt:

\Vert u+v \Vert^2 = \langle u+v, u+v \rangle.

Den inre produkten 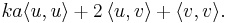ka\langle u, u \rangle + 2 \, \langle u, v \rangle + \langle v, v \rangle. Om vi uttrycker detta med hjälp av normen, så har vi fått ett bevis av den generella Pythagoras sats:

c^2 = a^2 + 2 \, \langle u, v \rangle + b^2; \qquad (*)

För att se detta skall man känna till att två vektorer säges vara ortogonala (vinkelräta) om deras inre produkt är noll:

\langle u, v \rangle = 0 \qquad \Longleftrightarrow \qquad u \quad och \quad v \quad ortogonala.

Med denna kunskap, tillsammans med sambandet (*) ovan, kan vi dra följande slutsats:

Vektorerna u och v är ortogonala om, och endast om, normerna av vektorerna u, v och u + v är relaterade enligt Pythagoras samband:
\langle u, v \rangle = 0 \qquad \Longleftrightarrow \qquad a^2 + b^2 = c^2.

Härmed är beviset av den generella Pythagoras sats fullbordat.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Pythagoras_sats"
Personliga verktyg