Från Rilpedia

För musikinstrumentet, se Triangel (musikinstrument).

---

En triangel (även trekant eller trehörning) är en geometrisk figur med många matematiska egenskaper.

En triangel består av en rand och ett triangelområde. Ett triangelområde är det område som bildas då tre icke-parallella linjer skär varandra. Skärningspunkterna kallas trianglens hörn. Sträckorna mellan hörnen är triangelns sidor. I varje hörn bildar sidorna en vinkel. I euklidisk geometri är summan av de tre vinklarna 180 grader (eller π radianer), ett samband som är intimt förknippat med parallellaxiomet. I en sfärisk triangel kan vinkelsumman vara större än 180 grader

Från varje hörn kan man dra en normal som är rätvinklig mot motstående sida. Denna sträcka kallas för en höjd. Det finns tre olika höjder i en och samma triangel, en från varje hörn. Den motstående sidan som nämndes ovan, kallas bas. I trubbvinkliga trianglar ligger två av höjderna inte inom triangeln, utan dras mot basens förlängning. Höjderna i en triangel skär varandra i en och samma punkt.

Från varje hörn kan man också dra en linje till motstående sidas mittpunkt. Denna sträcka kallas median. Medianerna skär varandra i en och samma punkt. Denna punkt kallas triangelns tyngdpunkt. En triangelformad pappskiva kan balanseras på sin tyngdpunkt. Om pappskivan hängs upp i ett hörn, kommer medianen från hörnet att gå lodrätt.

Från varje hörn kan man också dra en bisektris, det vill säga en linje som delar hörnvinkeln mitt itu. Bisektriserna skär varandra i samma punkt. Denna punkt kallas inskrivna cirkelns medelpunkt, eftersom det går att dra en cirkel som tangerar alla tre sidorna med centrum i denna punkt.

I varje sidas mittpunkt kan man dra en normal, den så kallade mittpunktsnormalen. De tre mittpunktsnormalerna skär varandra i samma punkt. Denna punkt kallas omskrivna cirkelns medelpunkt, eftersom det går att dra en cirkel som går genom alla tre hörnen med centrum i denna punkt. I en rätvinklig triangel ligger denna på hypotenusan, och i en trubbvinklig triangel ligger den utanför triangeln.

Speciella trianglar

En triangel är:

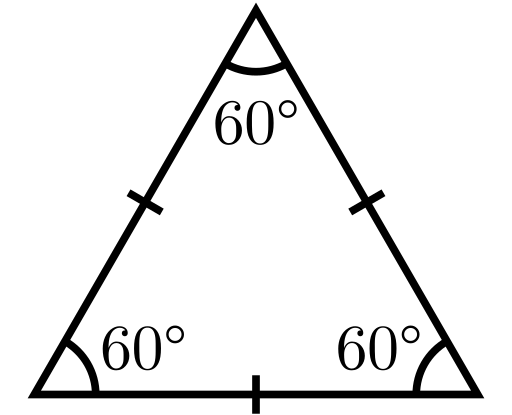
• Liksidig om alla sidor är lika långa
• Likbent om två sidor är lika långa
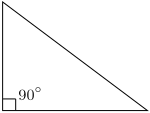
• Rätvinklig om en vinkel är rät (90 grader eller π / 2 radianer).
• Spetsvinklig om alla vinklar är mindre än 90 grader
• Trubbvinklig om en av vinklarna är större än 90 grader

Liksidig triangel är specialfall av likbent triangel.

En triangel kan vara både rätvinklig och likbent, och kan då kallas för en halv kvadrat.

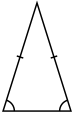Rätvinklig triangel	Liksidig triangel	Likbent triangel

Formler för triangel i euklidisk geometri

Formler för en triangel med basen b, övriga sidor a och c och höjden h.

Vinkelsumma	180 grader
Area	bh/2
Omkrets	a+b+c

• Arean av en liksidig triangel med sidan s är
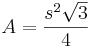
• Omkretsen av en liksidig triangel med sidan s är 3s
• Om en sida förlängs, bildas en yttervinkel vid det hörnet. I euklidisk geometri är denna yttervinkel lika stor som summan av de båda övriga hörnen (yttervinkelsatsen).

Se även

• Sierpinskitriangel
• Geometri
• Pythagoras sats
• Trigonometri
  • Areasatsen
  • Sinussatsen
  • Cosinussatsen
• Herons formel
• Polygoner
  • Kvadrat
  • Pentagon
• Cirkel
• Hyperbolisk triangel
• Sfärisk triangel