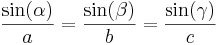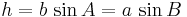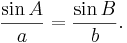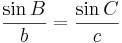Sinussatsen

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

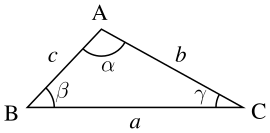
Sinussatsen är inom trigonometrin en sats om trianglar. För en triangel med sidlängderna a, b och c, och vinklarna mittemot dem som a med α o.s.v. enligt bild:

Triangle.Labels.svg

Då uttrycker sinussatsen att:

\frac{\sin(\alpha)}{a}=\frac{\sin(\beta)}{b}=\frac{\sin(\gamma)}{c}

Sinussatsen används främst inom triangulering när två vinklar och en sida är kända. Den kan också användas när två sidor och en av de andra vinklarna är kända.

Härledning

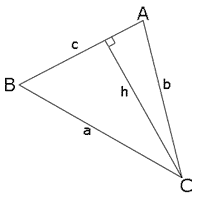
Law of sines proof.png

Rita en triangel med sidorna a, b, och c, och motstående vinklar A, B, och C. Dra en linje från vinkeln C till dess motstående sida c, som delar figuren i två rätvinkliga trianglar och beteckna denna linjes längd med h.

Man ser då att:

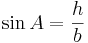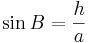
\sin A = \frac{h}{b} och \; \sin B = \frac{h}{a}

Vilket är ekvivalent med:

h = b\,\sin A = a\,\sin B

och

\frac{\sin A}{a} = \frac{\sin B}{b}.

Om linjen istället dras mellan vinkeln A och sidan a och samma procedur upprepas blir resultatet:

\frac{\sin B}{b} = \frac{\sin C}{c}

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Sinussatsen"
Personliga verktyg