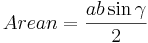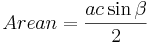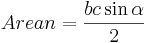Areasatsen

Texten från svenska Wikipedia

Areasatsen är en matematisk sats för att beräkna arean hos en godtycklig triangel då två sidor och en vinkel är kända.

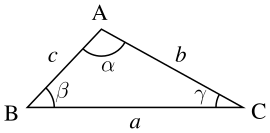
Antag att vi har en triangel med sidlängderna a, b och c. Dessutom betecknar vi vinklarna som står mittemot dessa sidor för α, β respektive γ.

Då gäller att arean för triangeln kan beräknas med någon av formlerna:

$Arean = {a b \sin\gamma \over 2}$

$Arean = {a c \sin\beta \over 2}$

$Arean = {b c \sin\alpha \over 2}$

Härledning

Titta på figuren. Arean av en triangel är lika med basen multiplicerat med höjden genom två, det vill säga:

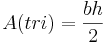
$A(tri) = {b h \over2}$

Med hjälp av trigonometri kan vi teckna följande samband mellan höjden, sidan a och vinkeln γ :

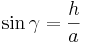
$\sin\gamma = {h \over a}$

Vilket är ekvivalent med $h = a sinγ$

Insättning av denna ekvation i den första ger:

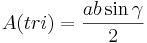
$A(tri) = {a b \sin\gamma \over2}$

Det vill säga Areasatsen.

Om vinkeln γ är trubbig gäller inte ovanstående. Man kan då med liknande resonemang komma fram till att:

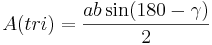
$A(tri) = {a b \sin(180 - \gamma)\over2}$

Men, då $sin(180 - v) = sin v$ leder även detta fram till att Areasatsen stämmer.