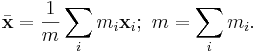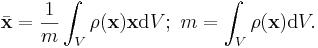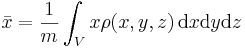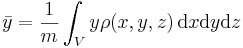Masscentrum
Från Rilpedia
Inom fysiken och dess tillämpningar är en kropps masscentrum positionen för det med avseende på delarnas massa viktade medelvärdet av beståndsdelarnas positioner. Positionen (relativt kroppen) för en kropps masscentrum är således en egenskap hos kroppen. Tyngdpunkten, å andra sidan, är den punkt där den resulterande kraften på en kropp som befinner sig i ett gravitationsfält kan anses angripa. Tyngdpunktens läge (relativt kroppen) beror således såväl på kroppens massfördelning som på egenskaperna hos det gravitationsfält kroppen befinner sig i, men i uniforma gravitationsfält sammanfaller båda punkterna.
I vissa fall kan man behandla en kropps massa som om den vore koncentrerad till dess masscentrum. Exempel är beräkning av lägesenergi för analys av stabilitet och beräkning av rörelsemängd vid kollisioner.
Innehåll |
Definition av masscentrum
Masscentrum för en grupp av punktmassor är det viktade medelvärdet av punkternas position. Vikten för varje punkt är punktens massa.
Om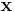 
representerar en godtycklig punkts läge relativt en referenspunkt origo, gäller att masscentrums läge relativt origo ges av
där summan löper över alla punktmassor som ingår i gruppen och m är gruppens totala massan.
Om ett system har en distribuerad densitet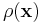 
inom ett volym V, definierar man på samma sätt:
De vektorekvationer som angivits ovan kan delas upp i skalära samband. Komponenterna av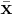 
i ett kartesiskt koordinatsystem är 
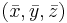som var och en kan beräknas med
.
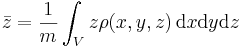Notera att läget hos referenspunkten origo inte har någon effekt på resultatet.
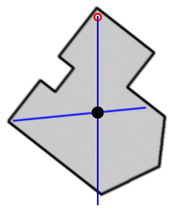
Dessa definitioner liknar definitionen av första centralmomentet för fördelningsfunktioner inom matematik, något som har samband med att man med tyngdpunktens läge kan bestämma vridmomentet av en distribuerad massa i ett uniformt gravitationsfält. Det ger också ett enkelt sätt att experimentellt bestämma tyndpunkten: vridmoment är noll när tyndpunkten ligger lodrät under en rotationspunkt. Tyngdpunkten ligger vid skärningspunkten av lodlinjer.
Exempel
Föremål som roterar, exempelvis de roterande delarna i en elmotor eller hjul på fordon som bilar, kallas statiskt balanserade om deras masscentrum ligger på rotationsaxeln. Detta är ett nödvändigt men inte tillräckligt villkor för att vibrationer ej ska uppstå. Föremålets övriga tröghetsegenskaper, dess tröghetsmoment, som beror på hur dess massa är fördelad, måste också uppfylla vissa krav. Att statisk balans är viktigt vet alla som betraktat centrifugeringsfasen på en tvättmaskin med horisontell axel. Då lägger sig gärna mycket tvätt i en klump och när varvtalet ökar kommer mer eller mindre kraftiga vibrationer att uppstå. Även packningen av tvätt i en centrifug med vertikal axel är känslig för ojämn fördelning av tvätten. Trots att centrifuger är konstruerade att tåla viss ojämn fördelning kan kraftiga vibrationer uppstå om tvätten är så fördelad att masscentrum hos kombinationen av centrifugens rotor och tvätten hamnat alltför långt ifrån centrifugens rotationsaxel. Oftast känner centrifugen av detta och stannar så tvätten kan packas om mer jämnt.
Balansen hos ett föremål som står på ett underlag bestäms av dess masscentrums läge, under förutsättning att gravitationsfältet har vissa egenskaper, vilket man med stor noggrannhet kan anta på jorden. För balans måste projektionen längs gravitationsfältet av masscentrums läge, ned på det underlag föremålet står på, befinna sig inom den yta som omgärdas av föremålets stödpunkter.
Ett flygplan som flyger påverkas av tryckkrafter från den omgivande luften, samt tyngdkraft från gravitationsfältet som det rör sig i. Om vi antar att gravitationsfältet ger upphov till ett parallellkraftfält, kommer momentet från gravitationskrafterna kring flygplanets masscentrum att vara noll. För att rotera flygplanet används krafter från den omgivande luften som ger upphov till ett moment. Då flygplanet ska flyga rakt fram utan att svänga måste det moment kring masscentrum, som krafterna från den omgivande luften ger upphov till, vara noll, åtminstone i medeltal. För att flygplanet ska vara stabilt måste de moment som uppstår då flygplanet utsätts för störningar, till exempel nos upp, vara sådana att störningen minskar. Eftersom krafter och moment på ett flygplan beror på dess form och fart, är det viktigt att konstruera och lasta flygplan så att dess masscentrum i flygfärdigt tillstånd ligger inom den volym, eller de gränser, som aerodynmiken medger. Om inte detta görs kan flygplanets vara omöjligt att flyga, alternativt bete sig onormalt, och olyckor kan lätt ske.
En kropp som rör sig har en rörelseenergi som är summan av rörelseenergin hos dess delar. För stela kroppar som endast rör sig rätlinjigt, det vill säga translaterar, kommer alla delar att ha samma hastighet. Därmed kan beräkningen av rörelseenergi förenklas till att omfatta en massa med masscentrums hastighet, vilket väsentligen behandlas som en partikel där
.
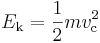För en kropp som endast roterar kommer rotationsrörelsen att innehålla energi. Denna energimängd kan för stela kroppar beräknas genom kunskap om kroppens vinkelhastighet och egenskaper hos kroppens massfördelning. För stela kroppar som både translaterar och roterar, kan totala energin beräknas som summan av translationsenergin hos en tänkt punktmassa med samma massa som kroppen och vars hastighet är samma som kroppens masscentrums hastighet, samt rotationsenergi som beräknas på samma sätt som för en stel kropp som endast roterar.
Icke-uniforma gravitationsfält
Om gravitationsfältet är konstant till storlek och riktning inom kroppens utsträckning, sammanfaller tyngdpunktens position med masscentrums position för godtyckliga kroppar. Gravitationsfältet kan dock inte alltid behandlas som om det vore konstant. Gravitationskraften från en massa avtar med avståndet i kvadrat, vilket varierar gravitationskraftens belopp. Kring ett gravitationscentrum är gravitationsfältet radiellt riktat, vilket innebär att även gravitationskraftens riktning varierar. Därmed kommer tyngdpunkten för kroppar som befinner sig i ett varierande gravitationsfält inte att sammanfalla med kropparnas masscentrum.
Då tyngdpunkten inte sammanfaller med masscentrum kan ett moment kring kroppens masscentrum uppstå på grund av de gravitationskrafter som kroppen utsätts för. Detta moment påverkar kroppens rörelse. För föremål på jorden är dessa moment mycket små och kan normalt försummas, speciellt i jämförelse med andra krafter och moment som kropparna påverkas av. För satelliter kan dock detta vara av stor betydelse. Då de övriga momenten som påverkar en satellit är mycket små, kan gravitationsinducerade moment ha en avgörande inverkan på stabiliteten för en satellits orientering.
