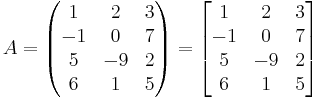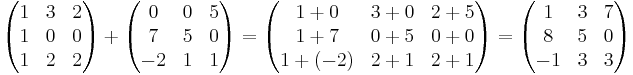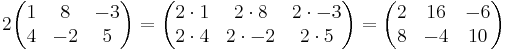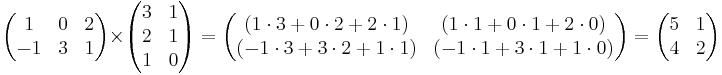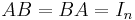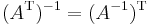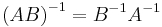Matris

Från Rilpedia

(Omdirigerad från Matrisinvers)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

För andra betydelser, se Matris (olika betydelser).

Inom matematiken är en matris ett rektangulärt schema av tal eller andra storheter. Den kan betraktas som en tensor av ordning 2, vilket betyder att varje element har bestämda regler vid räkneoperationer och att det finns två index. På en matris kan tre av de fyra grundläggande räknesätten utföras: addition, subtraktion och multiplikation, dock inte division. Därutöver finns vissa räkneoperationer som är specifika för matriser, till exempel transponering. Matriser kan användas för att hålla data som beror på två kategorier, och för att hålla ordning på koefficienterna i linjära ekvationssystem och vid linjära transformationer.

Innehåll

1 Definitioner och beteckningar
- 1.1 Exempel
2 Addition, subtraktion och multiplikation
3 Transponat
4 Kvadratiska matriser och relaterade dimensioner
5 Matrisinvers
- 5.1 Egenskaper hos inverterbara matriser
- 5.2 Icke kvadratiska matriser
6 Matriser med vissa egenskaper
- 6.1 Reellvärda matriser
- 6.2 Komplexvärda matriser
7 Se även

Definitioner och beteckningar

De horisontella raderna brukar benämnas just rader, medan de vertikala kallas kolumner eller kolonner. En matris med m rader och n kolumner kallas en m×n-matris (m gånger n-matris) och m och n kallas dess dimensioner.

Elementet (ett enskilt värde eller uttryck i matrisen) i en matris A (godtyckliga matriser betecknas normalt A, B och C) i den i:e raden och j:e kolumnen brukar betecknas med a_i,j eller A[i,j]. Det är vanligt att matriser avgränsas antingen med stora rundade parenteser eller med stora hakparenteser. (Avgränsning med enbart raka streck utan hakar brukar inte användas, för att undvika sammanblandning med determinanter.)

Exempel

Matrisen

$A = \begin{pmatrix} 1 & 2 & 3 \\ -1 & 0 & 7 \\ 5 & -9 & 2 \\ 6 & 1 & 5\end{pmatrix} = \begin{bmatrix} 1 & 2 & 3 \\ -1 & 0 & 7 \\ 5 & -9 & 2 \\ 6 & 1 & 5\end{bmatrix}$

är en 4×3-matris. Elementet A[2,3] eller a_2,3 är 7.

Addition, subtraktion och multiplikation

Addition

Huvudartikel: Matrisaddition

För att man skall kunna addera två matriser måste de ha samma dimensioner.

Om A och B är två m×n-matriser, så definieras C=A+B, som c_i,j=a_i,j+b_i,j.

Exempel:

$\begin{pmatrix} 1 & 3 & 2 \\ 1 & 0 & 0 \\ 1 & 2 & 2 \end{pmatrix} + \begin{pmatrix} 0 & 0 & 5 \\ 7 & 5 & 0 \\ -2 & 1 & 1 \end{pmatrix} = \begin{pmatrix} 1+0 & 3+0 & 2+5 \\ 1+7 & 0+5 & 0+0 \\ 1+(-2) & 2+1 & 2+1 \end{pmatrix} = \begin{pmatrix} 1 & 3 & 7 \\ 8 & 5 & 0 \\ -1 & 3 & 3 \end{pmatrix}$

Subtraktion

Helt analogt med additionen gäller att om A och B är två m×n-matriser, så definieras C=A − B, som c_i,j=a_i,j − b_i,j.

Multiplikation med skalär

Om en matris A och en skalär k är givna, definieras multiplikationen så att om B=kA gäller b_i,j=ka_i,j

Exempel:

$2 \begin{pmatrix} 1 & 8 & -3 \\ 4 & -2 & 5 \end{pmatrix} = \begin{pmatrix} 2\cdot 1 & 2\cdot 8 & 2\cdot -3 \\ 2\cdot 4 & 2\cdot -2 & 2\cdot 5 \end{pmatrix} = \begin{pmatrix} 2 & 16 & -6 \\ 8 & -4 & 10 \end{pmatrix}$

Matrismultiplikation

Multiplikation mellan två matriser är endast väldefinierad om antalet kolumner i den första är lika med antalet rader i den andra. Om A är en m×n-matris (m rader, n kolumner) och B en n×p-matris, så är produkten AB definierad, men om inte m=p, så är inte BA definierad. Om C=AB gäller då att

C_i,j=a_i,1 · b_1,j + a_i,2 · b_2,j + ... + a_i,n · b_n,j

för varje par i och j. Noterbart är att C är en m×p-matris.

Exempel:

$\begin{pmatrix} 1 & 0 & 2 \\ -1 & 3 & 1 \\ \end{pmatrix} \times \begin{pmatrix} 3 & 1 \\ 2 & 1 \\ 1 & 0 \end{pmatrix} = \begin{pmatrix} (1 \cdot 3 + 0 \cdot 2 + 2 \cdot 1) & (1 \cdot 1 + 0 \cdot 1 + 2 \cdot 0) \\ (-1 \cdot 3 + 3 \cdot 2 + 1 \cdot 1) & (-1 \cdot 1 + 3 \cdot 1 + 1 \cdot 0) \\ \end{pmatrix} = \begin{pmatrix} 5 & 1 \\ 4 & 2 \\ \end{pmatrix}$

Matrismultiplikation har följande egenskaper:

(AB)C = A(BC) för alla k×m-matriser A, m×n-matriser B och n×p-matriser C (”associativitet”).
(A + B)C = AC + BC för alla m×n matriser A och B samt n×k-matriser C (”distributivitet”).
C(A + B) = CA + CB för alla m×n-matriser A och B samt k×m-matriser C (”distributivitet”).

Det är viktigt att tänka på att kommutativitet normalt inte gäller; om A är en m×n-matris och B en n×m-matris så gäller normalt inte att AB=BA.

Matriser sägs vara antikommutativa om AB = −BA. Sådana matriser är viktiga i representationer av Lie-algebra och Clifford-algebra

Transponat

Huvudartikel: Transponat

Transponat är en typ av operation där man ändrar en matris dimensioner genom att flytta runt dess element. En m×n-matris A har således en n×m-matris som sitt transponat. En transponerad matris betecknas A^T. A^T[i,j]=A[j,i].

Exempel: 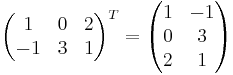$\begin{pmatrix} 1 & 0 & 2 \\ -1 & 3 & 1 \\ \end{pmatrix}^T = \begin{pmatrix} 1 & -1\\ 0 & 3 \\ 2 & 1 \\ \end{pmatrix}$

Det gäller även att (AB)^T=B^TA^T.

Kvadratiska matriser och relaterade dimensioner

En kvadratisk matris är en matris där antalet rader och kolumner är lika. De betecknas som n×n-matriser.

Enhetsmatriser, vilka betecknas I, eller I_n om man vill specifiera dimensionen, är matriser där elementen på diagonalen är 1 och övriga element 0. Med andra ord gäller att I[i,j]=1 om i=j och 0 om i ≠ j.

En kvadratisk matris A kallas inverterbar om det finns en matris B sådan att BA=I(=AB). B kallas A:s invers och betecknas A⁻¹. Även för vissa icke-kvadratiska matriser, A, kan man finna matriser B och C sådana att BA=I samt AC=I. Det gäller då i allmänhet att B ≠ C. B kallas då vänsterinvers och C högerinvers.

Om λ är ett tal och v en vektor sådana att Av=λv kallas v egenvektor och λ egenvärde till A. Varje kvadratisk matris har exakt n komplexa egenvärden.

Determinanten för en diagonaliserbar matris är produkten av dess n egenvärden. Inverterbara matriser är precis de som bara har nollskilda egenvärden.

Gauss–Jordan-elimination är en algoritm som kan användas för att beräkna en matris determinant, rank och egenvärden samt användas för att lösa linjära ekvationssytem.

En matris spår är summan av dess diagonalelement, vilken även är summan av dess egenvärden.

Alla ortogonala matriser är kvadratiska.

Genom att utnyttja formella Taylorserier kan ytterligare operationer göras på kvadratiska matriser. På så vis kan till exempel $e M$ definieras, givet vissa villkor på elementen i matrisen för att garantera konvergens.

Matrisinvers

En n×n-matris $A$ är inverterbar om det existerar en n×n matris $B$ sådan att

$AB = BA = I_n \$

Om detta är fallet så är matrisen $B$ entydigt bestämd av $A$ och kallas inversen till $A$ och betecknas $A - 1$ .

En kvadratisk matris som ej är inverterbar kallas singulär. En matris är singulär om och endast om dess determinant är lika med 0.

Egenskaper hos inverterbara matriser

Inversen av en inverterbar matris $A$ är också inverterbar med inversen

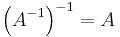$\left(A^{-1}\right)^{-1} = A$ .

Inversen av en inverterbar matris $A$ multiplicerad med en nollskild skalär $k$ är en produkt av inverserna av både matrisen och skalären

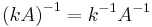$\left(kA\right)^{-1} = k^{-1}A^{-1}$ .

För en inverterbar matris $A$ är transponatet av inversen lika med inversen av transponatet

$(A^\mathrm{T})^{-1} = (A^{-1})^\mathrm{T} \,$

Produkten av två inverterbara matriser $A$ och $B$ av samma storlek är inverterbar med inversen

$\left(AB\right)^{-1} = B^{-1}A^{-1}$

(Observera att $A$ och $B$ har bytt plats.)

Icke kvadratiska matriser

Även för vissa icke-kvadratiska matriser, $A$ , kan man antingen finna en matris $B$ sådan att $B A = I$ , eller finna en matris $C$ sådan att $A C = I$ . $B$ respektive $C$ kallas då vänsterinvers respektive högerinvers. (Om en matris har både en vänsterinvers B och en högerinvers C, så måste $B$ = $C$ och vara invers till A, som av rangskäl därför måste vara kvadratisk.)

Matriser med vissa egenskaper

Reellvärda matriser

Matrisen $A$ är:

Kvadratisk om m=n.
Diagonal om $A i, j = 0$ då i och j är skilda.
Symmetrisk om $A T = A$ .
Skevsymmetrisk eller antisymmetrisk om $A T = - A$ .
Toeplitz om $A i, j$ endast beror på skillnaden i−j.
Triangulär om den är över- eller undertriangulär.
- Övertriangulär om $A i, j = 0$ om i>j.
- Undertriangulär om $A i, j = 0$ om i<j.
Ortogonal om $A T A = I$ .
Idempotent om $A 2 = A$ .
Nilpotent om den är kvadratisk och det finns ett heltal n sådant att $A n = 0$ .

Komplexvärda matriser

Matrisen $M$ är:

Unitär om $M H M = I$ , där $M H$ anger transponat och komplexkonjugering, kallas Hermiteskt konjugat.
Hermitesk (uttalas "hermitsk" eller "ermitsk", med tonvikt på i) om $M H = M$ . En Hermitesk matris är den komplexa motsvarigheten till en reell symmetrisk matris.

Se även

Matris

Från Rilpedia

Innehåll

Definitioner och beteckningar

Exempel

Addition, subtraktion och multiplikation

Addition

Subtraktion

Multiplikation med skalär

Matrismultiplikation

Transponat

Kvadratiska matriser och relaterade dimensioner

Matrisinvers

Egenskaper hos inverterbara matriser

Icke kvadratiska matriser

Matriser med vissa egenskaper

Reellvärda matriser

Komplexvärda matriser

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk