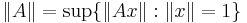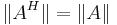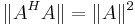Från Rilpedia

Det hermiteska konjugatet är en matematisk operation på en matris uppkallat efter franske 1800-talsmatematikern Charles Hermite.

Innehåll 1 Definition 2 Andra skrivsätt 3 Exempel 4 Egenskaper 5 Se även

Definition

Det hermiteska konjugatet av en matris 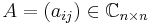definieras som 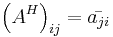där 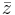betecknar komplexkonjugatet av z. Med andra ord är det hermiteska konjugatet till A definierat som A:s transponat med alla element komplexkonjugerade.

Notera att 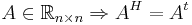, transponatet av A. Dvs, för reella matriser är det hermiteska konjugatet samma som vanlig transponering.

Andra skrivsätt

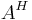skrivs även 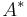eller .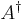

Exempel

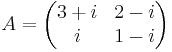
Ger att:

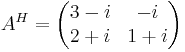
Egenskaper

Ur defintionen får man omedelbart följande egenskaper:

(A^H)^H = A

(A^H) ^{− 1} = (A ^{− 1})^H om A är inverterbar.

(A + B)^H = A^H + B^H

(λA)^H = λ ^* A^H, där λ ^* är λ:s komplexa konjugat.

(AB)^H = B^HA^H

Om operatornormen av A är:

så är

och

Se även

• Normal matris
• Hermitesk matris
• Symmetrisk matris
• Transponat