Hermitesk matris

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

En hermitesk matris, uppkallad efter franske 1800-talsmatematikern Charles Hermite, är inom matematiken den komplexa motsvarigheten till en symmetrisk matris.

Innehåll

Definition

En matris A säges vara hermitesk om AH = A, där AH betecknar den matris som fås av att ersätta A-transponat:s alla element med sina komplexa konjugat (det hermiteska konjugatet).

Exempel

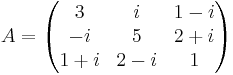
A= \begin{pmatrix} 3 & i & 1-i \\ -i & 5 & 2+i \\ 1+i & 2-i & 1 \end{pmatrix}

A är hermitesk, ty:

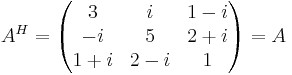
A^H = \begin{pmatrix} 3 & i & 1-i \\ -i & 5 & 2+i \\ 1+i & 2-i & 1 \end{pmatrix} = A

Reella egenvärden

En hermitesk matris har endast reella egenvärden.

Bevis

Låt A vara en hermitesk matris med icketrivial egenvektor x och tillhörande egenvärde λ, alltså Ax = λx.

Då A är hermitesk, dvs AH = A, får vi:

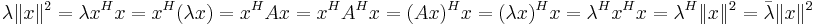
\lambda \|x\|^2= \lambda x^Hx= x^H(\lambda x)=x^HAx=x^HA^Hx=(Ax)^Hx=(\lambda x)^Hx=\lambda^H x^H x=\lambda^H\|x\|^2=\bar{\lambda} \|x\|^2

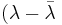(\lambda-\bar{\lambda})\|x\|^2=0

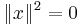
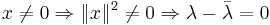
x\ne0 \Rightarrow \|x\|^2 \ne 0 \Rightarrow \lambda-\bar{\lambda}=0

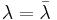\lambda =\bar{\lambda} dvs λ är reell

Hämtad från "https://sv.rilpedia.org/wiki/Hermitesk_matris"
Personliga verktyg