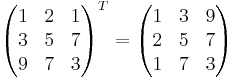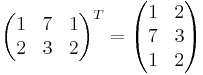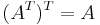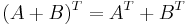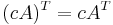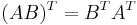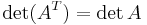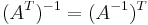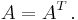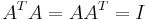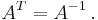Transponat
Från Rilpedia
I linjär algebra är transponatet av en matris A en annan matris betecknad AT. AT kan beräknas på följande ekvivalenta sätt:
- Låt A:s rader bilda AT:s kolonner.
- Låt A:s kolonner bilda AT:s rader.
- Bilda AT genom att reflektera A:s element i huvuddiagonalen.
Om aij är elementet på rad i, kolonn j i A, så ges elementen i AT av:
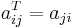 .
.
Innehåll |
Exempel
Egenskaper
Om A,B är matriser och c en skalär, så har man följande egenskaper:
- Transponatet är en involution:
- Transponatet är en linjär avbildning:
- Vid transponering av en produkt av matriser vänder man på ordningen:
- Determinanten är invariant för transponering:
- Om A är inverterbar är transponatet av inversen är inversen av transponatet:
- Om A endast har reella tal som element är ATA en positivt semidefinit matris.
Speciella matriser
Om D är en diagonalmatris är DT = D.
En symmetrisk matris är en matris där
En skevsymmetrisk matris är en matris där
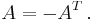 .
.
En ortogonal matris är en matris vars transponat är dess invers: