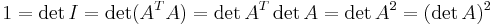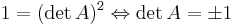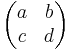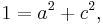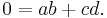Ortogonalmatris
Från Rilpedia
En ortogonalmatris är en reell kvadratisk matris med ortonormerade rader och kolonner. Det gäller för en ortogonal matris Q att 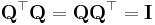 , det vill säga att transponatet av Q är invers till Q.
, det vill säga att transponatet av Q är invers till Q.
Ortogonalmatriser har konditionstal 1, varför de är viktiga för att få stabilitet vid numerisk linjär algebra.
Innehåll |
Exempel
Exempel på ortogonala matriser är:
- Alla enhetsmatriser.
- Alla permutationsmatriser.
Egenskaper
En reell kvadratisk matris av storlek n är ortogonal om och endast om dess kolumner bildar en ortonormerad bas för 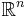 med den vanliga skalärprodukten införd. Om kolumnerna endast är ortogonala och inte normerade uppfyller matrisen ATA = D för någon diagonalmatris D istället.
med den vanliga skalärprodukten införd. Om kolumnerna endast är ortogonala och inte normerade uppfyller matrisen ATA = D för någon diagonalmatris D istället.
Determinanten till en ortogonal matris A är 1 eller -1:
Det omvända gäller dock inte; en matris med determinanten 1 är inte nödvändigtvis ortogonal.
En linjär avbildning som har en ortogonalmatris i en ON-bas är också en isometri. Vid basbyte mellan två ändliga ON-baser är basbytesmatrisen en ortogonalmatris, vilket gör att diagonalisering av vissa matriser blir väldigt enkelt, se spektralsatsen.
Ortogonalmatriser används vid ett antal matrisfaktoriseringar, exempelvis QR-faktorisering, polärfaktorisering och singulärvärdesfaktorisering.
Konstruktion
De enklaste ortogonala matriserna är (1) och ( − 1).
Ortogonala 2×2-matriser kan konstrueras genom ett antal ekvationer. Med beteckningarna:
Så vet vi att kolonnerna ska vara ortogonala med varandra, samt att varje kolonns skalärprodukt med sig själv ska vara 1. Detta ger ekvationerna:
De två första ekvationerna är ekvationen för en cirkel och om man låter a = cosθ och c = sinθ så får vi två möjliga lösningar b = − sinθ och d = cosθ eller b = sinθ och d = − cosθ. Detta ger matriserna:
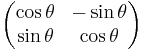 , en rotationsmatris.
, en rotationsmatris.
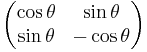 , en reflektionsmatris.
, en reflektionsmatris.