Från Rilpedia

Inom matematiken, specifikt linjär algebra, är en matrisfaktorisering en uppdelning av en matris i flera matriser på ett speciellt sätt. Det finns många sorters matrisfaktoriseringar, med tillämpningar inom olika sorters problem.

Innehåll 1 Faktoriseringar för att lösa linjära ekvationssystem 1.1 LU-faktorisering 1.2 Choleskyfaktorisering 1.3 QR-faktorisering 2 Uppdelningar med egenvärden och liknande 2.1 Diagonalisering 2.2 Jordans normalform 2.3 Singulärvärdesuppdelning

Faktoriseringar för att lösa linjära ekvationssystem

LU-faktorisering

Huvudartikel: LU-faktorisering

För alla kvadratiska matriser A, kan matrisen delas upp i så att A = LU för en nedåt triangulär matris L och en uppåt triangulär matris U. Detta kan sedan användas för att snabbare lösa ekvationssystem av typen Ax = b.

Choleskyfaktorisering

Choleskyfaktorisering kan ses som ett specialfall av LU-faktorisering; om matrisen A även är symmetrisk och positivt definit kan A uttryckas som A = U^TU för en uppåt triangulär matris U.

QR-faktorisering

Huvudartikel: QR-faktorisering

QR-faktorisering kan göras för alla 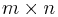-matriser A. Man uttrycker då matrisen A som A = QR för en ortogonal matris Q och en uppåt triangulär matris R. Då Q är ortogonal (Q ^{− 1} = Q^T) så ekvationssystemet Ax = b kan skrivas 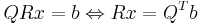, som är lättare att lösa.

Uppdelningar med egenvärden och liknande

Diagonalisering

Huvudartikel: Diagonalisering

Om en 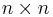-matris A har n egenvärden och lika många egenvektorer (om egenvärdena är distinkta så finns lika många egenvektorer), kan matrisen skrivas på formen A = TDT ^{− 1} där D är en diagonalmatris och T är en matris med egenvektorer. I vissa fall kan T göras till en ortogonal matris U så att A = UDU^T. Se även spektralsatsen.

Jordans normalform

Huvudartikel: Jordans normalform

För en given kvadratisk matris A blir jordans normalform A = TJT ^{− 1}, där T utgörs av As egenvektorer och J är en blockdiagonal matris. Varje block i J är bidiagonalt med As egenvärden i diagonalen och antigen ettor eller nollor i superdiagonalen. Diagonalisering är ett specialfall av jordans normalform.

Singulärvärdesuppdelning

Huvudartikel: Singulärvärdesuppdelning

Varje 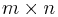-matris A kan singulärvärdesuppdelas, så att A = UDV^H för unitära matriser U och V och så att D har storleken 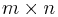och endast har värden (dessa värden kallas singulärvärden) i diagonalen. V^H betecknar det hermiteska konjugatet till V.