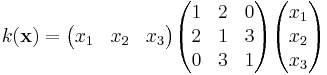Spektralsatsen

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Spektralsatsen är en samling matematiska satser inom den matematiska grenen linjär algebra. Satserna säger vilka linjära avbildningar som har en bas av ortonormerade egenvektorer och alltså kan diagonaliseras i denna bas, det vill säga huruvida matrisen A kan uttryckas som A = UDU * , där D är en diagonalmatris och U en unitär matris. Satsen säger dels att vissa matriser är diagonaliserbara, dels att man inte behöver räkna ut en invers, som man behöver vid allmänna diagonaliseringar, då matrisen skrivs A = TDT − 1.

Innehåll

Spektralsatser

Spektralsatsen finns i flera utföranden. Spektralsatsen för symmetriska avbildningar är oftast den enda som lärs ut i en grundkurs i linjär algebra.

Symmetriska avbildningar

Om V är ett ändligt-dimensionellt reellt euklidiskt rum gäller följande:

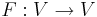F:V \rightarrow V är en symmetrisk linjär avbildning 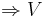\Rightarrow V har en ortonormerad bas av egenvektorer till F.

Hermitska avbildningar

Om V är ett ändligt-dimensionellt komplext euklidiskt rum gäller följande:

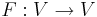F:V \rightarrow V är en hermitsk linjär avbildning 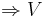\Rightarrow V har en ortonormerad bas av egenvektorer till F.

Normala avbildningar

Om V är ett ändligt-dimensionellt komplext euklidiskt rum gäller följande:

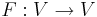F:V \rightarrow V är en normal linjär avbildning 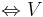\Leftrightarrow V har en ortonormerad bas av egenvektorer till F.

Notera ekvivalensen: Normala linjära avbildningar är alltså exakt de avbildningar som kan diagonaliseras med en bas av ortonormerade egenvektorer.

Bevis

Spektralsatsen bevisas för reella symmetriska avbildningar genom matematisk induktion.

  • Visar att satsen gäller inledningsvis. Dimensionen för rummet, 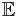\mathbb{E}, är då 1.

Vektorn 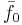\bar{f}_0 tillhör rummet 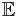\mathbb{E} och har längden (beloppet) 1 vilket ger att F:s avbildning av 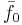\bar{f}_0 är en multipel av sig själv.

Vektorn 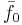\bar{f}_0 är alltså en egenvektor till F och därmed den sökta basen till rummet.


  • Antar vidare att satsen är sann för rum av dimensionen p, vilket åtminstone stämmer då dimensionen av rummet är 1 (enligt ovan).

Visar då att satsen även är sann för rum av dimensionen p + 1.


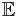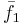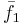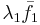Om λ1 är en reell rot till sekularekvationen för F i rummet \mathbb{E} och vektorn \bar{f}_1 är en egenvektor till F med längden 1. (Vilket är ekvivalent med att F:s avbildning av \bar{f}_1 blir \lambda_1 \bar{f}_1.)

Bildar mängden V som innehåller alla vektorer i 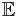\mathbb{E} som är ortogonala mot 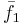\bar{f}_1. Dimensionen för V blir alltså p.

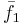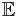Fyller ut \bar{f}_1 till en ON-bas för \mathbb{E}.

F:s matris i den basen blir då symmetrisk enligt: \begin{pmatrix} \lambda_1 & 0 & \cdots & 0 \\ 0 & \ddots & \cdots & a\\ \vdots & \vdots & \ddots & b \\ 0 & a & b & c \end{pmatrix}.

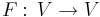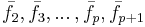Vi ser då att då F: \, V \rightarrow V så har V en ortonormerad bas bestående av egenvektorer till F :\, \bar{f}_2 , \bar{f}_3 , ...\, , \bar{f}_p , \bar{f}_{p+1}.

Det betyder i sin tur att 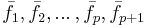\bar{f}_1 , \bar{f}_2 , ...\, , \bar{f}_p , \bar{f}_{p+1} är en ortonormerad bas bestående av egenvektorer till F


  • Satsen är sann inledningsvis och om den är sann för rum av dimensionen p så är den även sann för rum av dimensionen p + 1. Då är satsen sann i all oändlighet enligt induktionsaxiomet.

Historia

Spektralsatsen utformades under början av 1800-talet av Augustin-Louis Cauchy.

Tillämpningar

Kvadratiska former

En kvadratisk form kan skrivas som en symmetrisk matris, och kan därför diagonaliseras med en ortonormerad bas. Den blir då mer lätthanterlig. Spektralsatsen kan i vissa fall vara formulerad som att en kvadratisk form i ett euklidiskt rum har en kanonisk ortonormerad bas. Detta gör att spektralsatsen kan användas för att ta fram olika andragradsytors huvudaxlar.

Exempelvis kan den kvadratiska formen 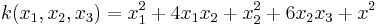k(x_1,x_2,x_3)= x_1^2 + 4x_1x_2 + x_2^2 + 6x_2x_3 + x^2 skrivas på matrisform som:

k(\mathbf{x}) = \begin{pmatrix} x_1 & x_2 & x_3 \end{pmatrix} \begin{pmatrix} 1 & 2 & 0 \\ 2 & 1 & 3 \\ 0 & 3 & 1 \\ \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}

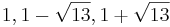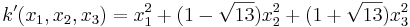som har egenvärdena 1, 1 - \sqrt{13}, 1+\sqrt{13}, så att k i den nya basen kan skrivas k'(x_1, x_2, x_3) = x_1^2 + (1 - \sqrt{13})x_2^2 + (1 + \sqrt{13})x_3^2.

Referenser

Hämtad från "https://sv.rilpedia.org/wiki/Spektralsatsen"
Personliga verktyg