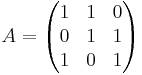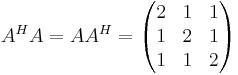Normal matris
Från Rilpedia
Inom matematiken är en normal matris en matris som kommuterar med sitt hermiteska konjugat
Definition
En kvadratisk matris A kallas normal om:
AHA = AAH
Där AH (även skrivet A * ) är det hermiteska konjugatet till A.
Exempel
Exempel på matriser som är normala är alla unitära och hermiteska (för komplexa matriser) och alla symmetriska och ortogonala matriser (för reella matriser).
Att reella symmetriska matriser är normala följer av att (då matrisen är reell blir det hermiteska konjugatet bara transponat):
- ATA = AA = AAT
För unitära matriser (AH = A − 1) följer det av att:
- AHA = A − 1A = I = AA − 1 = AAH
Dock behöver inte normala matriser vara hermiteska eller unitära. Exempel:
A är normal, men varken hermitesk eller unitär.