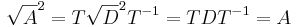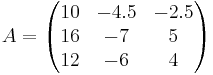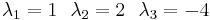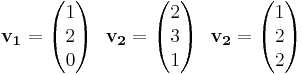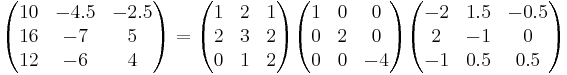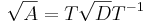Diagonalisering
Från Rilpedia
Diagonalisering är inom linjär algebra en omvandling av en matris till en diagonalmatris. En sådan omvandling sker med en transformationsmatris T, så att A = TDT − 1 för en matris A och en diagonalmatris D. Man säger att en matris är diagonaliserbar om den kan diagonaliseras, med andra ord är en matris A diagonaliserbar om det finns en matris T så att A = TDT − 1 för en diagonalmatris D.
Innehåll |
Villkor för diagonaliserbarhet
En matris A med format 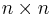 , med andra ord en linjär avbildning från ett vektorrum till sig själv
, med andra ord en linjär avbildning från ett vektorrum till sig själv 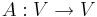 , är diagonaliserbar om och endast om summan av dimensionerna av dess egenrum är n. Detta inträffar då A har n egenvektorer som är en bas för vektorrummet. Då kan A uttryckas som A = TDT − 1, där T har As egenvektorer som kolonnvektorer och D har As egenvärden i diagonalen.
, är diagonaliserbar om och endast om summan av dimensionerna av dess egenrum är n. Detta inträffar då A har n egenvektorer som är en bas för vektorrummet. Då kan A uttryckas som A = TDT − 1, där T har As egenvektorer som kolonnvektorer och D har As egenvärden i diagonalen.
Egenvektorerna till en matris är en bas för hela rummet om alla egenvärden har en geometrisk multiplicitet som är lika med deras algebraiska multiplicitet, och alltså är en matris diagonaliserbar under dessa förutsättningarna.
Ett tillräckligt (men ej nödvändigt) villkor för att en matris med format 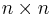 ska ha en bas av egenvektorer är att matrisen har n distinkta egenvärden
ska ha en bas av egenvektorer är att matrisen har n distinkta egenvärden
Speciella matriser
Nilpotenta matriser är ej diagonaliserbara, då de endast har egenvärdet 0. Detta skulle innebära att diagonalmatrisen skulle bli en nollmatris och A = TDT − 1 = 0, vilket inte är sant.
Projektioner är diagonaliserbara, och har talen 1 och 0 i diagonalen.
Enligt spektralsatsen är reella symmetriska matriser diagonaliserbara, och deras egenvektorer är ortogonala. Samma sak gäller för komplexa hermiteska matriser och normala matriser. Då egenvektorerna är ortogonala kan transformationsmatrisen skrivas som en ortogonal matris i det reella fallet och en unitär matris i det komplexa fallet, så att en symmetrisk matris kan skrivas A = TDTT, dvs med en transponerad istället för en inverterad transformationsmatris till höger, vilket är mycket lättare att räkna ut.
Exempeldiagonalisering
Vi diagonaliserar matrisen A:
Vi beräknar de tre egenvärdena:
Vi ser att de tre egenvärdena är distinkta, så vi vet att A är diagonaliserbar. Vi fortsätter med att beräkna egenvektorererna till egenvärdena:
Dessa bildar en bas för vektorrumet. Vi skapar matrisen T från vektorerna 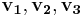 och räknar fram dess invers. Vi kan nu uttrycka A = TDT − 1:
och räknar fram dess invers. Vi kan nu uttrycka A = TDT − 1:
Tillämpningar
Om en matris A är diagonaliserbar, kan man använda det för att räkna fram potenser An effektivt, eftersom:
- A = TDT − 1
- A2 = (TDT − 1)2 = TDT − 1TDT − 1 = TDIDT − 1 = TD2T − 1
- An = TDnT − 1
Likartat kan man definiera kvadratroten ur en matris A som:
Där diagonalelementen i 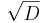 är roten ur Ds diagonalelement. Detta ger att:
är roten ur Ds diagonalelement. Detta ger att: