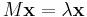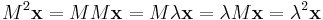Nilpotent matris

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Inom matematiken är en nilpotent matris en kvadratisk matris $M$ sådan att $M k = 0$ för något positivt heltal k.

Exempel

Matrisen $A$ nedan är nilpotent.

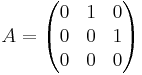
$A = \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{pmatrix}$

Eftersom $A 3 = 0$ :

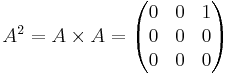
$A^2 = A \times A = \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$

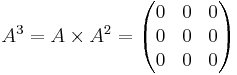
$A^3 = A \times A^2 = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$

Egenskaper

Låt $M$ vara en 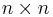$n \times n$ nilpotent matris:

För det minsta talet $k$ sådan att $M k = 0$ gäller att 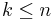$k \leq n$ .

$M$ :s alla egenvärden är noll, för om $λ$ är ett egenvärde till $M$ :

$M\mathbf{x} = \lambda\mathbf{x}$

Så gäller att:

$M^2\mathbf{x}=MM\mathbf{x} = M\lambda\mathbf{x} = \lambda M\mathbf{x} = \lambda^2\mathbf{x}$

och i förlängningen (genom matematisk induktion):

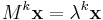$M^k\mathbf{x} = \lambda^k\mathbf{x}$ .

Men, då $M k = 0$ är vänsterledet noll, och alltså måste 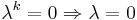$\lambda^k = 0 \Rightarrow \lambda = 0$ . Detta ger även att både $M$ :s determinant och spår är noll, samt att $M$ :s sekularpolynom är $λ n$

Nilpotent matris

Från Rilpedia

Exempel

Egenskaper

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk