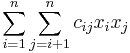Kvadratisk form

Från Rilpedia

Texten från svenska Wikipedia

En enmantlad hyperboloid som kan beskrivas av ekvationen ax² + by² − cz² = 1, dvs alla punkter (x,y,z) där den kvadratiska formen är lika med 1.

Kvadratisk form, matematik, kallas varje helt homogent uttryck, där varje term är av andra graden. Allmänt kan det skrivas

där c_ij är konstanter och x_i variabler.

Varje kvadratisk form av två variabler x och y kan alltså skrivas ax² + bxy + cy², för några tal a, b och c.

Formen kallas definit, om tecknet är detsamma för alla talpar x och y där ett av talen inte är noll. Till exempel är uttrycket ax² + bx² positivt definit, om a > 0 och b > 0 eftersom det är positivt för alla värden på x och y förutom då båda är noll. ax² för a > 0 är positivt semidefinit eftersom det är positivt eller noll för alla x och y.

Huruvida en kurva är negativt definit respektive positivt definit kan lättast ses genom kvadratkomplettering.

Teorin för de kvadratiska formerna, som bland annat sysselsätter sigmed frågan, hur den kvadratiska formen förhåller sig vid införande av nya variabler, är av grundläggande betydelse för de flesta områden av matematiken. Teoriens systematiska utveckling är väsentligen ett verk av 1800-talets matematiker, främst Carl Friedrich Gauss, Karl Weierstrass och Leopold Kronecker.

Denna artikel är helt eller delvis baserad på material från Nordisk familjebok, 1904–1926 ^(Not).