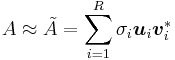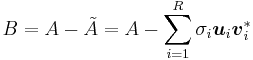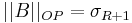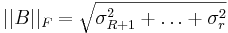Singulärvärdesuppdelning
Från Rilpedia
Inom linjär algebra är singulärvärdesuppdelning (eng. singular value decomposition, SVD), ibland kallat singulärvärdesfaktorisering eller singulärvärdesdekomposition, en sorts matrisfaktorisering. Alla reella och komplexa matriser kan faktoriseras med singulärvärdesuppdelning.
Innehåll |
Definition
För en matris A av storlek 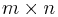 är singulrvärdesuppdelningen
är singulrvärdesuppdelningen
där U är en kvadratisk unitär 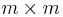 -matris, Σ en är en diagonal och icke-negativ
-matris, Σ en är en diagonal och icke-negativ 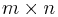 -matris och V * betecknar det hermiteska konjugatet till V, som är en unitär
-matris och V * betecknar det hermiteska konjugatet till V, som är en unitär 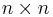 -matris. Matrisen Σ har singulärvärdena till A i sin diagonal, och vanlig praxis är att dessa singulärvärden ordnas i storleksordning med det största singulärvärdet först vänsterifrån i Σ.
-matris. Matrisen Σ har singulärvärdena till A i sin diagonal, och vanlig praxis är att dessa singulärvärden ordnas i storleksordning med det största singulärvärdet först vänsterifrån i Σ.
Singulärvärdesuppdelning är inte entydlig. Exempelvis är UK(m,m)Σ(VK(n,n)) * också en giltig uppdelning, där K(m,m) och K(n,n) är diagonalmatriser med eiθ i diagonalen, för godtyckligt värde på θ.
Singulärvärdesuppdelning på summaform
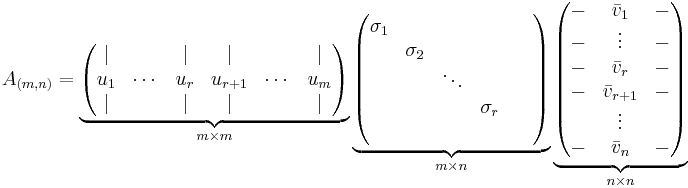
Man kan skriva om singulärvärdesuppdelningen A = UΣV * , där matrisen A har rang r, som en summa med r stycken matriser, så att varje matris i summan får rang 1, enligt nedan.
Här är σi singulärvärde nummer i till A, 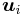 kolonnvektor i i U och
kolonnvektor i i U och 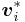 radvektor i i V.
radvektor i i V.
Tunn singulärvärdesuppdelning
Tunn singulärvärdesuppdelning fås genom att enbart beräkna de n vektorer i U som korresponderar med radvektorer i V * . Övriga kolumnvektorer i U beräknas inte, och därmer går det mycket snabbare att beräkna en tunn singulärvärdesuppdelning jämfört med en vanlig singulärvärdesuppdelning.
Matrisen Un blir då en 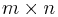 -matris, Σn en
-matris, Σn en 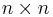 -matris och V en
-matris och V en 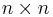 -matris.
-matris.
Tunn singulärvärdesuppdelning är i synnerhet mer beräkningseffektiv än vanlig singulärvärdesuppdelning om n < < m.
Kompakt singulärvärdesuppdelning
Kompakt singulärvärdesuppdelning fås genom att enbart beräkna de r kollumnerna i U och de r raderna i V * som korresponderar mot nollskillda singulärvärden. Då fås:
Här är Ur en 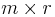 -matris, Σr en diagonal
-matris, Σr en diagonal  -matris och
-matris och 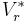 en
en 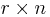 -matris.
-matris.
Kompakt singulärvärdesuppdelning är mer beräkningseffektiv än tunn singulärvärdesuppdelning om r < < n.
Beräkning
Metod anpassad för beräkning av människor
För en 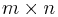 -matris A fås singulärvädesuppdelningen i ett fåtal steg. Man börjar med att beräkna den kvadratiska matrisen A * A. Varför man gör detta syns tydligare om man skriver om A med singulärvärdesuppdelning:
-matris A fås singulärvädesuppdelningen i ett fåtal steg. Man börjar med att beräkna den kvadratiska matrisen A * A. Varför man gör detta syns tydligare om man skriver om A med singulärvärdesuppdelning:
Spektralsatsen för hermiteska matriser säger att alla hermiteska matriser M kan skrivas som M = WΛW * , där Λ är en diagonal matris med egenvärdena till matrisen M i diagonalen. Kolonnvektorerna till W utgörs av egenvektorerna till matrisen M , som i sin tur utgör en ortonormerad bas. Notera att eftersom M är en hermitesk matris har den enbart reella egenvärden.
Eftersom A * A är en hermitesk matris ((A * A) * = A * A * * = A * A) har vi alltså likheten
Eftersom singulärvärdena till A är positiva (alltså är | σi | = σi) ser man att dessa fås genom att ta roten ur egenvärdena till A * A, dessutom ser man att V fås genom att beräkna egenvektorer till matrisen A * A.
Med A, V och Σ kända beräknas U enkelt genom att ställa upp AV = UΣ. Eftersom Σ är en diagonal matris är det enkelt att beräkna likheten. Ifall, för 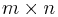 -matrisen A,
-matrisen A, 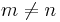 eller ifall matrisen A inte har full rang kommer några kolonner inte att fås i detta steg, eftersom de multipliceras med 0. Dessa kolonnvektorer väljs då med fördel så att matrisen U blir unitär.
eller ifall matrisen A inte har full rang kommer några kolonner inte att fås i detta steg, eftersom de multipliceras med 0. Dessa kolonnvektorer väljs då med fördel så att matrisen U blir unitär.
Alternativt kan man beräkna U genom att ställa upp AA * , då har man istället V som obekant och V kan beräknas som förklaras ovan. Man kan även beräkna U samt V separat genom att ställa upp A * A och AA * , denna metod innebär dock oftast mer arbete då man måste beräkna egenvektorer till två matriser.
Exempel
Man börjar med att beräkna A * A.
Nu beräknar man egenvärden och egenvektorer till A * A genom att ställa upp det karakteristiska polynomet, för exempel på detta se artikeln om egenvärden och egenvektorer. Vi får egenvärdena till 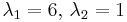 , och därmed blir singulärvärdena
, och därmed blir singulärvärdena 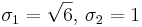 . Vi får egenvektorerna (normerade) enligt nedan:
. Vi får egenvektorerna (normerade) enligt nedan:
Nu beräknar man U med hjälp av sambandet AV = UΣ
Man ser att 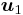 kommer multipliceras med
kommer multipliceras med 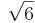 , att
, att 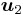 kommer multipliceras med 1 och att
kommer multipliceras med 1 och att 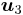 kommer multipliceras med 0. Nu väljer man
kommer multipliceras med 0. Nu väljer man 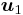 och
och 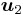 så att likheten AV = UΣ gäller,
så att likheten AV = UΣ gäller, 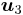 väljs ortogonal mot
väljs ortogonal mot 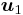 och
och 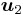 .
.
Alltså har vi vår singulärvärdesuppdelning enligt nedan.
Singulärvärdesuppdelningen på vanlig form:
Singulärvärdesuppdelningen på summaform:
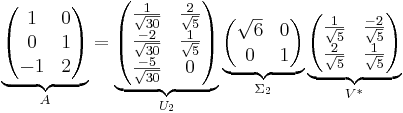
Singulärvärdesuppdelningen på tunn form:
Numerisk beräkningsmetod
Singulärvärdesuppdelningen till en matris A beräknas typiskt i två steg. I det första steget reduceras A till en bidiagonal matris. Detta tar O(mn2) flyttalsoperationer, om 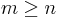 .
.
Det andra steget går ut på att beräkna singulärvärdesuppdelningen till denna bidiagonala matris. Detta steg beräknas iterativt med en bestämd precision. Om denna precision antas konstant tar det andra steget O(n) iterationer, som var kostar O(n) flyttalsoperationer. Därmed är det första steget det dyrare, och den totala kostnaden är O(mn2) flyttalsoperationer.
Tillämpningar
Beräkning av pseudoinvers
Man kan enkelt beräkna Moore-Penrose pseudoinvers, betecknat 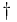 nedan, till en matris A med hjälp av singulärvärdesuppdelning. Om A har singulärvärdesuppdelning enligt A = UΣV * fås Moore-Penrose pseudoinvers till A enligt nedan.
nedan, till en matris A med hjälp av singulärvärdesuppdelning. Om A har singulärvärdesuppdelning enligt A = UΣV * fås Moore-Penrose pseudoinvers till A enligt nedan.
Här beräknar man Σ† genom att först ta inversen av varje nollskillt singulärvärde i Σ, de singulärvärden som var 0 i Σ förblir 0 i Σ†, och sedan transponerar man resultatet. Moore-Penrose pseudoinvers används bland annat för att lösa linjära minstakvadratproblem.
Bestämning av de fyra fundamentala underrummen samt rang
Man kan enkelt bestämma rang samt de fyra fundamentala underrummen (värderummet och nollrummet till en given matris och matrisens hermiteska konjugat) till en matris A genom att titta på matrisens singulärvärdesuppdelning. Antag en singulärvärdesuppdelning enligt nedan, där σ1 till σr är samtliga nollskillda singulärvärden.
Då fås följande:
Approximation med matris av lägre rang
En vanlig tillämpning av singulärvärdesuppdelning är att approximera en given matris med en annan liknande matris av lägre rang. Om man vill approximera en matris A av rang r med en matris 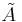 , som har rang R, där R < r, fås
, som har rang R, där R < r, fås 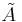 med hjälp av singulärvärdesuppdelningen på summaform enligt nedan:
med hjälp av singulärvärdesuppdelningen på summaform enligt nedan:
I de flesta tillämpningar är felet viktigt, vi betecknar felet B enligt följande.
Genom operatornorm eller frobeniusnorm av B fås felet vid approximationen 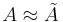 , dessa normer kan enkelt beräknas med hjälp av singulärvärdena enligt vad som visas nedan. Vilken av normerna som är bäst lämpad för feluppskattningen beror på tillämpning.
, dessa normer kan enkelt beräknas med hjälp av singulärvärdena enligt vad som visas nedan. Vilken av normerna som är bäst lämpad för feluppskattningen beror på tillämpning.
Denna metod för approximation används inom många tillämpningar, bland annat inom signalbehandlning. Om man t.ex. har brus av storleksordningen σR + 1 så kan man slänga bort termer som är små jämfört med bruset så att 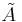 ger en förbättrad signal.
ger en förbättrad signal.
Andra vanliga användningsområden
- Förstärkning (norm)
- Principalkomponentanalys
- Polärfaktorisering
Se även
Referenser
- Treil, Sergei. Linear Algebra Done Wrong, 2004, Brown University. Tillgänglig: http://www.math.brown.edu/~treil/index.html




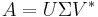
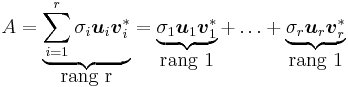
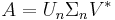
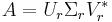
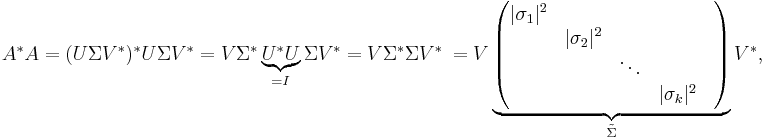
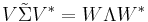
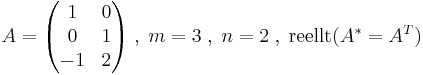
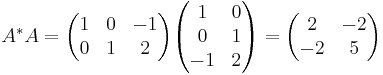
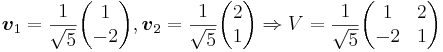
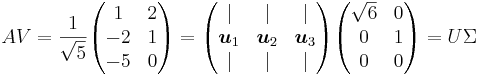
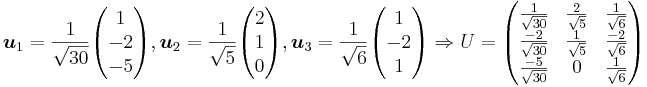
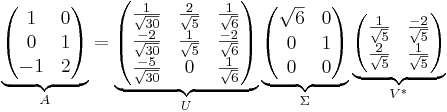
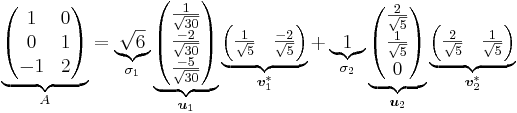
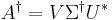
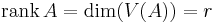
![V(A)= N(A^*)^{\perp} = \left[ \begin{pmatrix} | \\ u_{1} \\ | \end{pmatrix}, \, \begin{matrix} \\ \cdots \\ \end{matrix} \, , \begin{pmatrix} | \\ u_{r} \\ | \end{pmatrix} \right] \, \sub \, \mathbb{C}^m](/w/images/sv.rilpedia.org/math/b/9/4/b943542e7882c0c0cee8eef9b69ebc74.png)
![V(A^*) = N(A)^{\perp} = \left[ \begin{pmatrix} | \\ v_{1} \\ | \end{pmatrix}, \, \begin{matrix} \\ \cdots \\ \end{matrix} \, , \begin{pmatrix} | \\ v_{r} \\ | \end{pmatrix} \right] \, \sub \, \mathbb{C}^n](/w/images/sv.rilpedia.org/math/9/0/e/90e520b3f7d26661f59e9151f302d814.png)
![N(A) = V(A^*)^{\perp} = \left[ \begin{pmatrix} | \\ v_{r+1} \\ | \end{pmatrix}, \, \begin{matrix} \\ \cdots \\ \end{matrix} \, , \begin{pmatrix} | \\ v_{n} \\ | \end{pmatrix} \right] \, \sub \, \mathbb{C}^n](/w/images/sv.rilpedia.org/math/6/6/2/66247ec4c6da8b0c3930b1d2dadc12e2.png)
![N(A^*) = V(A)^{\perp} = \left[ \begin{pmatrix} | \\ u_{r+1} \\ | \end{pmatrix}, \, \begin{matrix} \\ \cdots \\ \end{matrix} \, , \begin{pmatrix} | \\ u_{m} \\ | \end{pmatrix} \right] \, \sub \, \mathbb{C}^m](/w/images/sv.rilpedia.org/math/f/2/0/f209eb67e5e52e9a5606ff94e2682ced.png)