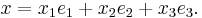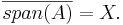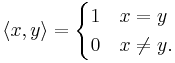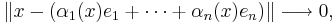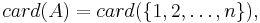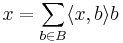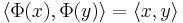Ortonormerad bas

Från Rilpedia

Texten från svenska Wikipedia

Inom matematik är begreppet ortonormal bas en generalisering till så kallade pre-Hilbertrum av det faktum att i det euklideska rummet 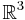$\mathbb{R}^3$ kan varje vektor $x = (x 1, x 2, x 3)$ skrivas som en summa av sina komposanter:

$x = x_1e_1 + x_2e_2 + x_3e_3.\,$

I denna summa ger enhetsvektorerna $e 1 = (1,0,0)$ , $e 2 = (0,1,0)$ och $e 3 = (0,0,1)$ upphov till ett rektangulärt koordinatsystem i 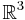$\mathbb{R}^3$ . I detta sammanhang är det mängden av enhetsvektorer ${e 1, e 2, e 3}$ som utgör en ortonormal bas för det euklideska rummet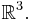 $\mathbb{R}^3.$

(Skalärkroppen, $F$ , till de vektorrum $(X, F)$ som behandlas i denna artikel antas vara mängden av komplexa tal 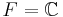$F = \mathbb{C}$ .)

Innehåll

1 Definition

Definition

Linjärt spann

Låt 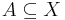$A \subseteq X$ vara en delmängd till ett vektorrum $X$ . Det linjära spannet av $A$ är den mängd, $s p a n (A)$ , som består av alla linjärkombinationer

$\xi_1x_1 + \cdots + \xi_nx_n,$

vars koefficienter $ξ k$ är komplexa tal och vars komponenter $x k$ är element i mängden $A$ .

Total mängd

En delmängd 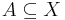$A\subseteq X$ till ett normerat rum, $X$ , är en total mängd om det slutna höljet av dess linjära spann utgör hela rummet $X$ ; det vill säga om

$\overline{span(A)} = X.\,$

Ortonormal mängd

En delmängd 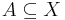$A \subseteq X$ till ett pre-Hilbertrum $X$ , säges vara en ortonormal mängd om den inre produkten 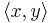$\langle x,y\rangle$ mellan två element 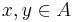$x,y \in A$ är

$\langle x,y\rangle = \begin{cases}1 & x = y\\0 & x \neq y.\end{cases}$

Ortonormal bas

En delmängd 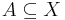$A \subseteq X$ till ett pre-Hilbertrum $X$ , säges vara en ortonormal bas till $X$ om $A$ är en total, ortonormal mängd.

Exempel på ortonormerade baser:

mängden {(1,0,0),(0,1,0),(0,0,1)} ger en ortonormal bas på R³
mängden {f_n : n ∈ Z} med f_n(x) = exp(2πinx) ger en ortonormerad bas på det komplexa rummet L²([0,1])
mängden {e_b : b ∈ B} med e_b(c) = 1 om b=c och 0 i övrigt ger en ortonormerad bas på rummet l²(B).

Schauderbas

En sekvens 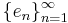$\{e_n\}_{n=1}^\infty$ av element i ett normerat rum $X$ , säges vara en Schauder bas för $X$ om varje element 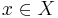$x\in X$ kan associeras med en sekvens 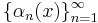$\{\alpha_n(x)\}_{n=1}^\infty$ av komplexa tal, sådan att normen

$\Vert x - (\alpha_1(x)e_1 + \cdots + \alpha_n(x)e_n) \Vert \longrightarrow 0,$

då heltalet 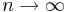$n \to \infty$ .

Ett normerat rum $X$ som besitter en Schauder bas är separabelt. Omvändningen till detta påstående är emellertid inte sant, då det finns separabla Banachrum som inte besitter någon Schauder bas. Detta resultat bevisades så sent som 1973 av P. Enflo, som gav en explicit konstruktion av ett separabelt Banachrum som saknar Schauder bas.

Linjärt oberoende mängd

En delmängd 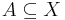$A \subseteq X$ av ett vektorrum $X$ , säges vara linjärt oberoende, om elementen 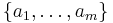$\{a_1,\dots,a_m\}$ i varje ändlig delmängd av $A$ besitter följande egenskap: Det enda sättet på vilket en godtycklig linjärkombination

$c_1a_1 + \cdots + c_m a_m$

kan var noll, är om samtliga koefficienter c_k är noll.

Hamelbas

Låt $X$ vara ett vektorrum och 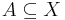$A\subseteq X$ en linjärt oberoende delmängd. Denna delmängd säges vara en Hamel bas för $X$ om dess linjära spann utgör mängden $X$ , det vill säga om

s p a n (A) = X .

Med hjälp av Zorns lemma kan man visa att varje vektorrum 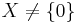$X \neq \{0\}$ har en Hamel bas.

Dimension för vektorrum

Låt $A$ och $B$ vara två godtyckliga Hamelbaser för samma vektorrum $X$ . Då gäller det att $A$ och $B$ har samma kardinalitet: $c a r d (A) = c a r d (B)$ .

Om det finns ett naturligt tal $n$ sådant att

$card(A) = card(\{1,2,\dots,n\}),$

så säger man att vektorrummet $X$ är ändlig-dimensionellt och att dess dimension $d i m (X) = n$ ; i annat fall säger man att $X$ är ett oändlig-dimensionellt vektorrum.

I matematiken är en ortonormerad bas i ett inre produktrum (även: vektorrum med inre produkt) en mängd element som spänner upp en tät delmängd i rummet och som är parvis ortogonala och av längd 1. Notera att en ortonormerad bas är i allmänhet inte en "bas", det vill säga det är i allmänhet inte möjligt att ange varje element i rummet som en ändlig linjärkombination av baselement. Detta är varför definitionen ovan endast kräver att rummet som spänns upp av den ortonormala basen är tät i vektorrummet, inte att det är lika med hela rummet. Inte heller är det möjligt att tala om en ortonormerad bas i varje vektorrum, såvida det inte har en inre produkt först. Allmänna Banachrum har till exempel inte någon ortonormerad bas. I vissa Banachrum kan man dock införa en Schauderbas, som i viss mån är en motsvarighet till en ortonormerad bas för dessa rum.

Exempel på ortonormerade baser:

mängden {(1,0,0),(0,1,0),(0,0,1)} ger en ortonormal bas på R³
mängden {f_n : n ∈ Z} med f_n(x) = exp(2πinx) ger en ortonormerad bas på det komplexa rummet L²([0,1])
mängden {e_b : b ∈ B} med e_b(c) = 1 om b=c och 0 i övrigt ger en ortonormerad bas på rummet l²(B).

Notera att i det oändligdimensionella fallet, så kommer en ortonormerad bas inte bli en bas i samma mening som i linjär algebra; för att skilja dem åt så kallas baser i oändligdimensionella rum för Hamelbaser.

Genom att använda Zorns lemma så kan man visa att varje Hilbertrum kan ges minst en ortonormerad bas; dessutom: två ortonormerade baser i ett rum har samma kardinalitet. Ett Hilbertrum är separabelt omm det finns en uppräknelig ortonormerad bas.

Om B är en ortonormerad bas i H så kan varje element x i H skrivas som

$x=\sum_{b\in B}\langle x,b\rangle b$

och normen av x ges av

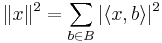$\|x\|^2=\sum_{b\in B}|\langle x,b\rangle |^2$ .

Även om B är ouppräknelig så kommer endast ett ändligt antal termer i summan vara skilda från noll, och uttrycket är därmed väldefinierat. Summan kallas även Fourierutvecklingen av x.

Om B är en ortonormerad bas i H, så är H isomorf med l²(B) i följande mening: det existerar en bijektiv linjär avbildning Φ : H -> l²(B) sådan att

$\langle\Phi(x),\Phi(y)\rangle=\langle x,y\rangle$

för alla x och y i H.

Ortonormerad bas

Från Rilpedia

Innehåll

Definition

Linjärt spann

Total mängd

Ortonormal mängd

Ortonormal bas

Schauderbas

Linjärt oberoende mängd

Hamelbas

Dimension för vektorrum

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk