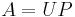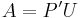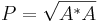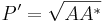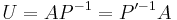Från Rilpedia

Polärfaktorisering är inom linjär algebra en matrisfaktorisering som är analog till polärfaktorseringen av ett komplext tal, z = re^iθ, där r är absolutbeloppet av z och θ är z:s argument.

Definiton och beräkning

Givet en matris A kan den faktoriseras på formen:

som kallas högerpolärfaktorisering. A kan även faktoriseras som:

som kallas vänsterpolärfaktorisering eller omvänd polärfaktorisering.

U är en unitär matris som är gemensam för båda faktoriseringarna. P och P' är positivt semidefinita hermiteska matriser. Faktoriseringarna existerar alltid och är unika så länge A är inverterbar och P väljs att vara positivt definit.

Matriserna P och P' ges av:

där A ^* är det hermiteska konjugatet till A. Uttrycken är väldefinierade då A ^* A och AA ^* är positivt definita hermiteska matriser, så att det existerar en unik kvadratrot.

Matrisen U ges sedan alltid av:

Beräkning via singulärvärdesfaktorisering

Om A är singulärvärdesfaktoriserad, A = WΣV ^* , ges matriserna i polärfaktoriseringarna av:

U = WV ^*

P = VΣV ^*

P' = WΣW ^*