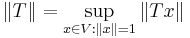Operatornorm
Från Rilpedia
Inom matematiken är en operatornorm ett sätt att tilldela en "storlek" till vissa linjära operatorer. Operatornormen kan ses som den maximala förlängingen av en vektor som en linjär avbildning kan göra.
Innehåll |
Bakgrund och definition
En linjär operator  (där V och W är normerade rum) sägs vara begränsad om det finns ett positivt reellt tal c så att
(där V och W är normerade rum) sägs vara begränsad om det finns ett positivt reellt tal c så att
för alla 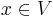 . För att visa att en linjär operator är begränsad kan man hitta ett c så att
. För att visa att en linjär operator är begränsad kan man hitta ett c så att
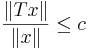 .
.
För alla 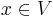 , med andra ord ett supremum. Detta supremum är operatornormen för T, betecknad
, med andra ord ett supremum. Detta supremum är operatornormen för T, betecknad 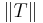 , alltså
, alltså
 .
.
Operatornormen kan även uttryckas som
vilket kommer av att T är en linjär avbildning.
Egenskaper
Operatornormen uppfyller de vanliga kraven för normer:
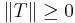 och
och 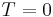 omm
omm 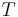 är en nollavbildning.
är en nollavbildning.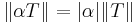
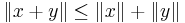
Man kan även se att:
Exempel
Enhetsavbildning
En enhetsavbildning 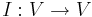 där
där  är begränsad och har norm
är begränsad och har norm 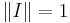 .
.
Matriser
En reell matris A med format 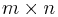 kan ses som en linjär avbildning
kan ses som en linjär avbildning 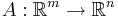 . A är begränsad och flera normer kan införas, se matrisnorm.
. A är begränsad och flera normer kan införas, se matrisnorm.