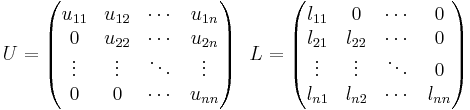Triangulär matris

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Inom matematiken är en triangulär matris en kvadratisk matris som har endast nollor på ena sidan om diagonalen.

Innehåll

Definitioner

Man säger att en matris är uppåt triangulär, övertriangulär eller högertriangulär om endast talen ovanför och i diagonalen är nollskilda. I en nedåt triangulär, undertriangulär eller vänstertriangulär matris är endast talen i och under diagonalen nollskilda.

Matrisen U är uppåt triangulär medan matrisen L är nedåt triangulär:

U = \begin{pmatrix} u_{11} & u_{12} & \cdots & u_{1n} \\ 0 & u_{22} & \cdots & u_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & u_{nn} \end{pmatrix} ~~ L = \begin{pmatrix} l_{11} & 0 & \cdots & 0 \\ l_{21} & l_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & 0 \\ l_{n1} & l_{n2} & \cdots & l_{nn} \end{pmatrix}

En strikt triangulär matris har nollskilda element endast på ena sidan om diagonalen, med andra ord är även diagonalen noll. Det finns alltså strikt uppåt triangulära matriser och strikt nedåt triangulära matriser. Alla strikt triangulära matriser är nilpotenta.

Egenskaper

  • En matris som är både uppåt och nedåt triangulär är en diagonalmatris.
  • En transponerad uppåt triangulär matris är en nedåt triangulär matris och vice versa.
  • Determinanten av en triangulär matris är produkten av diagonalelementen. Detta kan ses genom att man utvecklar efter första rad eller kolonn hela tiden.
  • Beräkningar är lätta att utföra på triangulära matriser, vilket utnyttjas t.ex. vid LU-faktorisering.
  • En matris som är både normal och triangulär är diagonal.
  • Varje komplex kvadratisk matris kan genom basbyte uttryckas som en triangulär matris enligt Schurs sats. Med Jordans normalform kan den skrivas på en ännu enklare, triangulär, form.

Tillämpningar

Ekvationsystemlösning

Om man har ett ekvationssystem med en nedåt (eller uppåt) triangulär triangulär matris som vänsterled; 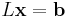L\mathbf{x} = \mathbf{b} löses denna snabbt genom bakåtsubstition. Ekvationsystem blir:

l11x1 = b1
l21x1 + l22x2 = b2
...
ln1x1 + ... + lnnxn = bn

Lösningen ges då av att man först räknar fram vad x1 blir, sätter in den i nästa ekvation, osv:

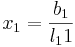
x_1 = \frac{b_1}{l_11}
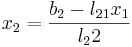
x_2 = \frac{b_2-l_{21}x_1}{l_22}
...
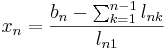
x_n = \frac{b_n - \sum_{k=1}^{n-1}l_{nk}}{l_{n1}}

Detta används t.ex. vid ekvationssystemlösning med LU-faktorisering.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Triangul%C3%A4r_matris"
Personliga verktyg