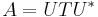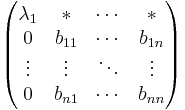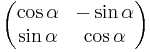Schurs sats

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Schurs sats är en matematisk sats inom linjär algebra. Satsen är uppkallad efter den judiske matimatikern Issai Schur(1875 - 1941) som studerade bl.a under Frobenius. Satsen säger att alla 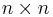n \times n-matriser, i någon bas, kan representeras av en uppåt triangulär matris.

Innehåll

Schurs sats

Låt 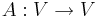A:V \rightarrow V vare en linjär avbildning och V vara ett (komplext) vektorrum. Då finns det en Ortonormerad bas för V så att A i denna bas representeras av en uppåt triangulär matris, det vill säga alla 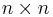n \times n matriser kan skrivas på formen

A = U T U^{*}\,

där U är en unitär matris (inversen av u är lika med det hermiteska konjugatet för U, U − 1 = U * ) och T är en uppåt triangulär matris med egenvärden till A på diagonalen.

Bevis

Satsen bevisas genom matematisk induktion.
Låt V vara ett vektorrum och 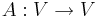A: V \rightarrow V vara en linjär avbildning.

  • Satsen är sann om dim(V) = 1 (då en 1 \times 1 matris är uppåt triangulär).
  • Antag att satsen är sann då dim(V) = n − 1.

Låt 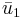\bar{u}_1 vara en normerad egenvektor till A som hör till egenvärdet λ1, dvs

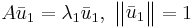A\bar{u}_1 = \lambda_1 \bar{u}_1,\ \begin{Vmatrix}\bar{u}_1\end{Vmatrix} = 1.

Låt nu W vara det ortogonala komplimentet till 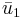\bar{u}_1,

W = \left[ \bar{u}_1 \right]^{\perp}.

Dimensionen för W blir då dim(V) − 1 = n − 1.
Låt vektorerna 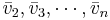\bar{v}_2, \bar{v}_3, \cdots, \bar{v}_n vara en ortonormerad bas för W.
Då utgör 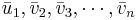\bar{u}_1, \bar{v}_2, \bar{v}_3, \cdots, \bar{v}_n en ortonormerad bas för V.
I denna bas representeras A av matrisen

\begin{pmatrix}\lambda_1 & * & \cdots & * \\ 0 & b_{11} & \cdots & b_{1n} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & b_{n1} & \cdots & b_{nn}\end{pmatrix}

Första kolonnen består endast av egenvärdet λ1 följt av nollor. Alla element till höger om λ1 på första raden är ointressanta.
Däremot låter vi det nedre högra blocket definiera en ny avblidning B:W \rightarrow W .
Då dim(W) = n − 1 så finns enligt antagandet en ortonormerad bas 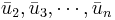\bar{u}_2, \bar{u}_3, \cdots, \bar{u}_n för W så att B övergår i uppåt triangulär form i denna bas, vilket medför att även A, i basen 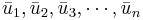\bar{u}_1,\bar{u}_2, \bar{u}_3, \cdots, \bar{u}_n, övergår uppåt i triangulär form.

Anmärkningar

  • Även om man utgår från en reell matris så kan matriserna U och T ha komplexa element.

t.ex rotationsmatrisen

\begin{pmatrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{pmatrix}

har endast komplexa egenvärden, och då T har egenvärden på diagonalen så kommer T i detta fall ha komplexa värden på diagonalen.

  • Om A är en normal matris (A = A * ) så är matrisen T diagonal med egenvärden på diagonalen. Därmed så kan Schurs sats ses som en utvidgning av spektralsatsen.
  • Om två matriser kommuterar (AB = BA) så kan de skrivas om med samma bas, dvs A = UTAU * och B = UTBU * med samma unitära matris U.

Referenser

  • Sergei Treil, Linear Algebra Done Wrong, Kapitel 6, Brown University, 2004
Hämtad från "https://sv.rilpedia.org/wiki/Schurs_sats"
Personliga verktyg