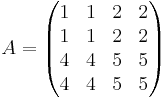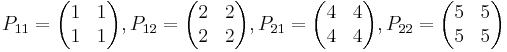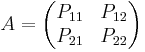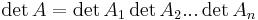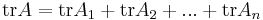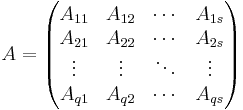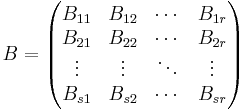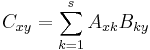Blockmatris

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Inom matematiken är en blockmatris en uppdelning av en matris i mindre matriser. Den ursprungliga matrisen kan då skrivas som en samling mindre matriser. Uppdelningen av en matris i block måste vara konsistent, man kan se det som att man inför vertikala och horisontella linjer som går genom hela matrisen.

Exempel

Matrisen:

A= \begin{pmatrix} 1 & 1 & 2 & 2 \\ 1 & 1 & 2 & 2 \\ 4 & 4 & 5 & 5 \\ 4 & 4 & 5 & 5 \end{pmatrix}

Kan delas upp i fyra 2x2-matriser:

P_{11} = \begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix} , P_{12} = \begin{pmatrix} 2 & 2 \\ 2 & 2 \end{pmatrix} , P_{21} = \begin{pmatrix} 4 & 4 \\ 4 & 4 \end{pmatrix} , P_{22} = \begin{pmatrix} 5 & 5 \\ 5 & 5 \end{pmatrix}

Så att A då kan skrivas:

A = \begin{pmatrix} P_{11} & P_{12} \\ P_{21} & P_{22} \end{pmatrix}

Blockdiagonala matriser

En blockdiagonal matris är en kvadratisk matris som har kvadratiska matriser i diagonalen, men alla andra element är noll. Om A är blockdiagonal kan den skrivas på formen:

A = \begin{pmatrix} A_1 & 0 & \cdots & 0 \\ 0 & A_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & A_n \end{pmatrix}

Där Ak är en kvadratisk matris. Matrisen A kan då skrivas som en direkt summa, 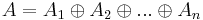A = A_1 \oplus A_2 \oplus ... \oplus A_n . Det finns även samband för determinanten och spåret:

\det{A} = \det{A_1} \det{A_2} ... \det{A_n} \,
\operatorname{tr}{A} = \operatorname{tr}{A_1} + \operatorname{tr}{A_2} + ... + \operatorname{tr}{A_n}

Blockmatrismultiplikation

Given två blockmatriser matriserna A och B där A har format 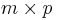m \times p och B har format 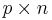p \times n , med blockindelning:

A = \begin{pmatrix} A_{11} & A_{12} & \cdots & A_{1s} \\ A_{21} & A_{22} & \cdots & A_{2s} \\ \vdots & \vdots & \ddots & \vdots \\ A_{q1} & A_{q2} & \cdots & A_{qs} \end{pmatrix}
B = \begin{pmatrix} B_{11} & B_{12} & \cdots & B_{1r} \\ B_{21} & B_{22} & \cdots & B_{2r} \\ \vdots & \vdots & \ddots & \vdots \\ B_{s1} & B_{s2} & \cdots & B_{sr} \end{pmatrix}

Dvs, A har s kolonnupdelningar och q raduppdelningar. B har r kolonnupdelningar och s raduppdelningar.

Man kan då räkna ut matrisprodukten C = AB med format 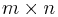m \times n , med q raduppdelningar och r kolonnupdelningar med:

C_{xy} = \sum_{k = 1}^s A_{xk} B_{ky}
Hämtad från "https://sv.rilpedia.org/wiki/Blockmatris"
Personliga verktyg