Idempotent
Från Rilpedia
Inom matematiken och datavetenskapen säger man att en operation är idempotent om avbildningen resulterar i samma resultat hur många gånger man än applicerar den. Ett element a sägs vara ett idempotent element med avseende till en binär operator * om a * a = a.
Innehåll |
Definition
Unära operatorer
Om f är en idempotent unär operator på mängden S gäller att, för alla 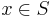 :
:
- f(f(x)) = f(x)
Binära operatorer
En binär operator * sägs vara idempotent på en mängd S om, för alla 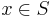 :
:
- x * x = x
I datavetenskap
Inom datavetenskap avser en idempotent subrutin eller funktion en subrutin som inte ändrar systems tillstånd. Om man exempelvis har ett databassystem skulle en idempotent subrutin exempelvis kunna vara en subrutin som hämtar det namn och den adress som hör till ett visst kundnummer, en subrutin som inte är idempotent skulle exempelvis kunna vara en subrutin som lägger in en lagd order i systemet.
Exempel
Idempotenta funktioner
- Absolutbelopp av komplexa eller reella tal är en idempotent unär operator:
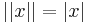 .
. - En funktion av två variabler som ger det största värdet tillbaka är idempotent: max(x,x) = x.
- Projektioner i vektorrum är idempotenta unära operatorer, när man har projicerat på värderummet ändras inte vektorn efter flera projiceringar (projektioner brukar t.o.m. definieras som idempotenta linjära avbildningar).
Idempotenta element
Bland heltalen (och även rationella och reella talen) är 1 idempotent med avseende på multiplikation och 0 är idempotent med avseende på addition.
I en grupp finns inga idempotenta element förutom det neutrala elementet.
I en ring sägs ett element vara idempotent om det är idempotent med avseende på multiplikationen. Varje idempotent element i en ring är även en nolldelare, eftersom a(1 − a) = 0. Man kan exempelvis betrakta ringen av heltal modulo 6. I den här ringen finns fyra idempotenta element: 0, 1, 3 och 4.



