Från Rilpedia

I matematikområdet ringteori är en nolldelare ett element a i en ring, sådant att ekvationen ax = 0 har en lösning x ≠ 0. Ofta krävs också att a ≠ 0. En ring är nolldelarfri om den saknar nollskilda nolldelare.

Om ringen inte är kommutativ skiljer man på vänsternolldelare, som är element a så att ax = 0 är lösbart, och högernolldelare, som är element a så att xa = 0 är lösbart.

Exempel

De vanliga talområdena, såsom heltalen, de reella talen, de komplexa talen, med flera, är nolldelarfria, eftersom man där har regeln att produkter av nollskilda element är nollskilda:

Om a och b är två "vanliga tal", och   a ≠ 0 ≠ b,   så är också   ab ≠ 0.

Däremot är exempelvis matrisen 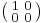i matrisringen av 2×2-matriser med reella element en nolldelare, eftersom

.

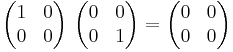Produkten av två kvadratiska matriser kan alltså bli nollmatrisen, trots att ingen av dem själva är nollmatrisen. I denna ring består nolldelarna av matriserna med determinant noll.

Egenskaper

En nolldelare kan aldrig vara en enhet, det vill säga att en nolldelare är inte inverterbar, för om ax = 0 följer det att:

0 = a ^{− 1}0 = a ^{− 1}ax = x

Alla idempotenta element 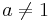är nolldelare, för om a² = a följer det att a(a − 1) = (a − 1)a = 0.

Alla nilpotenta element är nolldelare, för om aⁿ = 0 följer det att aa^{n − 1} = a^{n − 1}a = 0.

Ringen av kongruensklasser modulo n, 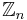, har nolldelare om och endast om n är ett sammansatt tal.

Se även

• Kancelleringslagen