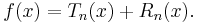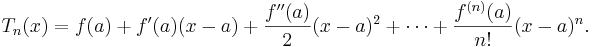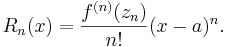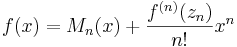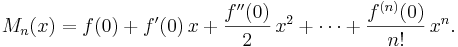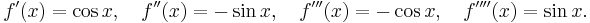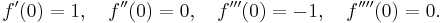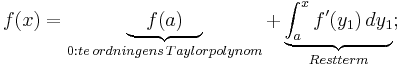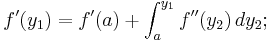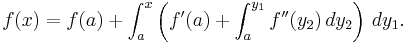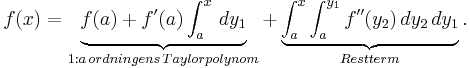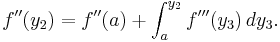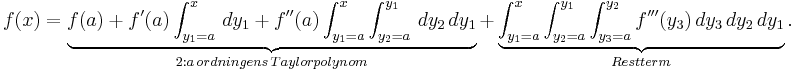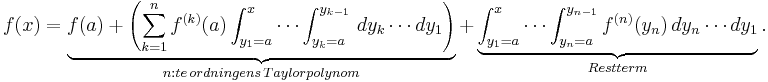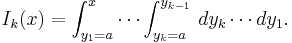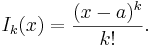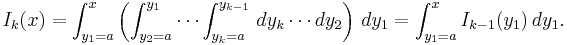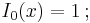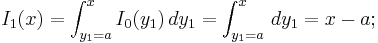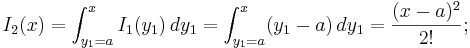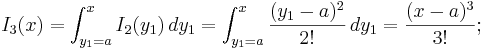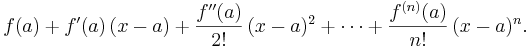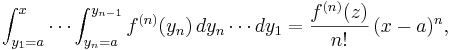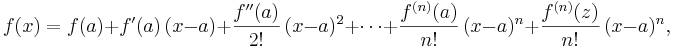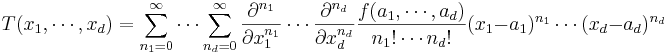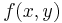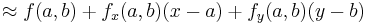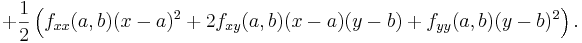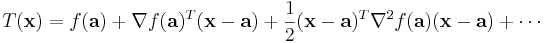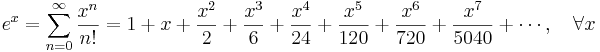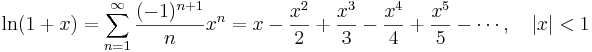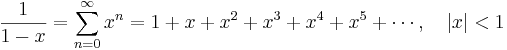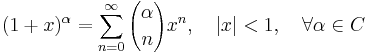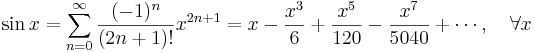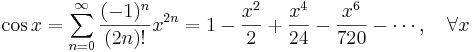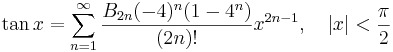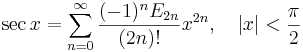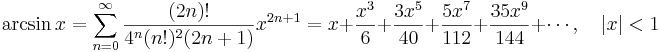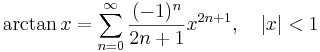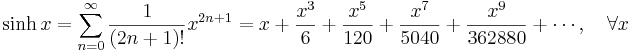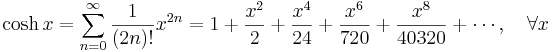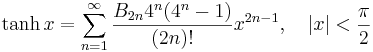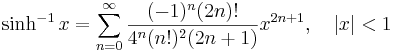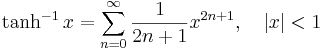Taylorserie

Från Rilpedia

(Omdirigerad från Mac-Laurin serie)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

När graden av Taylorutvecklingen stiger, närmar den sig den rätta funktionen. Bilden visar sin(x) och Taylorapproximationer, polynom av grad 1, 3, 5, 7, 9, 11 och 13.

Inom matematik är en Taylorutveckling av en funktion, f(x), ett sätt att framställa den som ett polynom, för värden på argumentet x som ligger i närheten av en fixerad punkt a. Taylorutvecklingen har fått sitt namn efter den engelske matematikern Brook Taylor. Om den fixerade punkten a väljs att vara talet noll, talar man om Maclaurinutvecklingen av funktionen, efter Colin Maclaurin.

Innehåll

1 Definition
- 1.1 Maclaurinutvecklingen
2 Exempel: Maclaurinpolynom för sinus-funktionen
3 Tillämpning
4 Härledning av Taylorpolynom
5 Egenskaper
6 Taylorutveckling i flera variabler
7 Lista över Maclaurinserier
8 Historia
9 Referenser

Definition

Om symbolen n betecknar ett positivt heltal, så kan en Taylorutveckling av ordning n för en funktion f skrivas på följande sätt:

$f(x) = T_n(x) + R_n(x).\,$

Funktionen $T n$ är det så kallade Taylorpolynomet av ordning n, associerad med funktionen f:

$T_n(x) = f(a) + f^\prime(a)(x-a) + \frac{f^{\prime\prime}(a)}{2}(x-a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n.$

Den andra termen i Taylorutvecklingen kallas Lagranges restterm (efter Louis Lagrange) och ger information om hur väl funktionen f approximeras av Taylorpolynomet:

$R_n(x) = \frac{f^{(n)}(z_n)}{n!}(x-a)^n.$

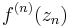Symbolen $f^{(n)}(z_n)\,$ betecknar den n:te derivatan av funktionen f, beräknad i punkten $z n$ , och symbolen n! betecknar n fakultet: produkten av alla positiva heltal som är mindre än eller lika med n. Det positiva heltalet n kan väljas godtyckligt – förutsatt att funktionen har derivator av alla ordningar – och för varje val av talet kommer $z n$ att vara ett tal som ligger någonstans mellan talen x och a; exakt var $z n$ ligger vet man inte, och detta är en nackdel med att Taylorutveckla en funktion.

Maclaurinutvecklingen

Maclaurinutvecklingen skrivs

$f(x) = M_n(x) + \frac{f^{(n)}(z_n)}{n!}x^n$

där $z n$ är ett tal som ligger någonstans mellan talen x och noll.

$M_n(x) = f(0) + f^\prime(0) \, x + \frac{f^{\prime\prime}(0)}{2}\, x^2 + \cdots + \frac{f^{(n)}(0)}{n!} \, x^n.$

Exempel: Maclaurinpolynom för sinus-funktionen

Vi skall beräkna de fem första Maclaurinpolynomen för den trigonometriska funktionen

f (x) = sin x

, då argumentet x befinner sig i närheten av punkten a=0. För detta behöver vi känna till derivatorna till sinus-funktionen, av ordningarna ett, två, tre och fyra:

$f^\prime(x) = \cos x, \quad f^{\prime\prime}(x) = -\sin x, \quad f^{\prime\prime\prime}(x) = -\cos x, \quad f^{\prime\prime\prime\prime}(x) = \sin x.$

Om vi beräknar dessa för argumentet x=0, så ser vi att derivatorna av jämn ordning är lika med noll:

$f^\prime(0) = 1, \quad f^{\prime\prime}(0) = 0, \quad f^{\prime\prime\prime}(0) = -1, \quad f^{\prime\prime\prime\prime}(0) = 0.$

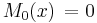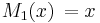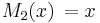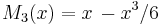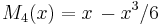De fem första Maclaurinpolynomen för sinus-funktionen är därför: $M_0(x) \,= 0$ , $M_1(x) \,= x$ , $M_2(x) \,= x$ , $M_3(x) = x \,- x^3/6$ , $M_4(x) = x \,- x^3/6$ .

Tillämpning

Taylorutvecklingar är speciellt användbara då vissa funktioner, som till exempel de trigonometriska eller logaritmen, vilka normalt är svåra att evaluera, kan approximeras med godtycklig noggrannhet av deras trunkerade Taylorutvecklingar på ett visst intervall.

Härledning av Taylorpolynom

Taylorutveckligen av en funktion vilar på den så kallade analysens fundamentalsats, som förenar de två begreppen derivata och integral av en funktion:

$f(x) = \underbrace{\quad f(a) \quad}_{0:te \, ordningens \, Taylorpolynom} + \underbrace{\int_a^x f^\prime(y_1) \, dy_1}_{Restterm};$

Symbolen 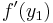$f^\prime(y_1)$ betecknar derivatan av funktionen $f$ , beräknad i punkten $y 1$ .

På samma sätt som för funktionen $f (x)$ kan vi tillämpa Analysens fundamentalsats på derivatan 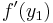$f^\prime(y_1)$ :

$f^\prime(y_1) = f^\prime(a) + \int_a^{y_1} f^{\prime\prime}(y_2) \, dy_2;$

Symbolen 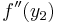$f^{\prime\prime}(y_2)$ betecknar andraderivatan (derivatan av derivatan) av funktionen f, beräknad i punkten $y 2$ .

Vi sätter in detta uttryck för derivatan 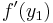$f^\prime(y_1)$ i framställningen av funktionen $f (x)$ :

$f(x) = f(a) + \int_a^x \left(f^\prime(a) + \int_a^{y_1}f^{\prime\prime}(y_2) \, dy_2\right) \, dy_1.$

Eftersom a är ett fixerat tal kommer 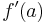$f^\prime(a)$ också att vara ett fixerat tal; Det kan därför brytas ut från integralen med avseende på variabeln $y 1$ :

$f(x) = \underbrace{f(a) + f^\prime(a) \int_a^x \, dy_1}_{1:a \, ordningens \, Taylorpolynom} + \underbrace{\int_a^x \int_a^{y_1} f^{\prime\prime}(y_2) \, dy_2 \, dy_1}_{Restterm}.$

Liksom för derivatan kan vi uttrycka andraderivatan som en integral av den så kallade tredjederivatan:

$f^{\prime\prime}(y_2) = f^{\prime\prime}(a) + \int_a^{y_2}f^{\prime\prime\prime}(y_3) \, dy_3.$

Sätter vi in detta i ovanstående framställning av funktionen $f (x)$ får vi 2:a ordningens Taylorpolynom med restterm:

$f(x) = \underbrace{f(a) + f^\prime(a) \int_{y_1=a}^x \, dy_1 + f^{\prime\prime}(a)\int_{y_1=a}^x \int_{y_2=a}^{y_1} \, dy_2 \, dy_1}_{2:a \, ordningens \, Taylorpolynom} + \underbrace{\int_{y_1=a}^x \int_{y_2=a}^{y_1} \int_{y_3=a}^{y_2}f^{\prime\prime\prime}(y_3) \, dy_3 \, dy_2 \, dy_1}_{Restterm}.$

Samma procedur kan tillämpas på tredjederivatan 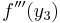$f^{\prime\prime\prime}(y_3)$ för att ge Taylorpolynomet av tredje ordningen tillsammans med en restterm, och så vidare.

På detta sätt kan man i princip härleda Taylorpolynomet av godtycklig ordning tillsammans med en motsvarande restterm; Notera att resttermerna ger information om hur väl de respektive Taylorpolynomen approximerar funktionen f:

$f(x) = \underbrace{f(a) + \left(\sum_{k=1}^n f^{(k)}(a)\int_{y_1=a}^x \cdots \int_{y_k=a}^{y_{k-1}} \, dy_k \cdots dy_1\right)}_{n:te \, ordningens \, Taylorpolynom} + \underbrace{\int_{y_1=a}^x \cdots \int_{y_n=a}^{y_{n-1}}f^{(n)}(y_n) \, dy_n \cdots dy_1}_{Restterm}.$

Multipel-integraler

Vi ser att Taylorpolynomen är uppbyggda av så kallade multipel-integraler:

$I_k(x) = \int_{y_1=a}^x \cdots \int_{y_k=a}^{y_{k-1}} \, dy_k \cdots dy_1.$

Vi skall visa att var och en av dessa multipel-integraler i själva verket är polynom:

$I_k(x) = \frac{(x-a)^k}{k!}.$

(Se artikeln om fakultet för en beskrivning av symbolen $k!$ .) För detta skriver vi om uttrycket för $I k (x)$ som en integral av den närmast föregående multipel-integralen $I k - 1 (x)$ :

$I_k(x) = \int_{y_1=a}^x \left(\int_{y_2=a}^{y_1} \cdots \int_{y_k=a}^{y_{k-1}} \, dy_k \cdots dy_2 \right)\, dy_1 = \int_{y_1=a}^x I_{k-1}(y_1) \, dy_1.$

Om vi vet hur multipel-integralen $I k - 1 (x)$ ser ut så kan vi beräkna multipel-integralen $I k (x)$ .

Nollte ordningens multipel-integral definieras som talet ett:

$I_0(x) = 1\,;$

Första ordningens multipel-integral:

$I_1(x) = \int_{y_1=a}^x I_0(y_1) \, dy_1 = \int_{y_1=a}^x \, dy_1 = x-a;$

Andra ordningens multipel-integral:

$I_2(x) = \int_{y_1=a}^x I_1(y_1) \, dy_1 = \int_{y_1=a}^x (y_1-a) \, dy_1 = \frac{(x-a)^2}{2!};$

Tredje ordningens multipel-integral:

$I_3(x) = \int_{y_1=a}^x I_2(y_1) \, dy_1 = \int_{y_1=a}^x \frac{(y_1-a)^2}{2!} \, dy_1 = \frac{(x-a)^3}{3!};$

Taylorpolynomet av ordning n

Sammanfattningsvis kan vi skriva Taylorpolynomet av ordning n, associerat med funktionen f, på följande form:

$f(a) + f^\prime(a) \, (x-a) + \frac{f^{\prime\prime}(a)}{2!} \, (x-a)^2 + \cdots + \frac{f^{(n)}(a)}{n!} \, (x-a)^n.$

Lagranges restterm

Om vi använder oss av den så kallade Lagranges medelvärdessats (en av de viktigaste satserna inom matematisk analys) kan vi skriva resttermen på ett betydligt enklare sätt än som en komplicerad multipel-integral:

$\int_{y_1=a}^x \cdots \int_{y_n=a}^{y_{n-1}}f^{(n)}(y_n) \, dy_n \cdots dy_1=\frac{f^{(n)}(z)}{n!} \, (x-a)^n,$

där z är ett tal som ligger någonstans mellan talen x och a. (Exakt var z ligger vet vi inte.)

Taylorutveckling av en funktion

Avslutningsvis kan vi skriva funktionen f(x) som en summa av ett Taylorpolynom och dess associerade Lagranges restterm:

$f(x) = f(a) + f^\prime(a) \, (x-a) + \frac{f^{\prime\prime}(a)}{2!} \, (x-a)^2 + \cdots + \frac{f^{(n)}(a)}{n!} \, (x-a)^n + \frac{f^{(n)}(z)}{n!} \, (x-a)^n,$

där z är ett tal som ligger någonstans mellan talen x och a.

Egenskaper

Om Taylorutvecklingen för en funktion konvergerar för varje x i intervallet (a − r, a + r) och om summan är lika med f(x), så är funktionen f(x) analytisk på intervallet. För att kontrollera om serien konvergerar mot f(x), så använder man i normalfallet uppskattningar av resttermen som anges i Taylors sats. En funktion är analytisk omm den kan skrivas som en potensserie; koefficienterna i denna potensserie är då nödvändigtvis de som ges i Taylorutvecklingen ovan. Det finns dock funktioner som saknar Taylorutveckling men som ändå är analytiska.

Betydelsen av sådana potensserier ligger i tre punkter. För det första sker derivering och integrering av potensserier term för term och är därmed speciellt lätt. För det andra kan en analytisk funktion på ett unikt sätt utvidgas till en holomorf funktion som definieras på en öppen skiva i det komplexa talplanet, vilket gör att hela maskineriet från den komplexa analysen blir tillgänglig. Och för det tredje kan en trunkerad Taylorutveckling användas för att beräkna approximationer av funktionsvärden.

Funktionen f(x)=e^-1/x² om x ≠ 0; f(0)=0 är inte analytisk: Taylorutvecklingen är 0, fastän själva funktionen inte är det.

Observera dock att det finns exempel på oändligt deriverbara funktioner f(x) vars Taylorutveckling konvergerar, men som inte konvergerar mot f(x). Till exempel, för den funktion f(x) som definieras genom f(x) = exp(−1/x²) if x ≠ 0 och f(0) = 0, är alla derivator noll i punkten x=0, så Taylorutvecklingn av f(x) är noll, med oändlig konvergensradie, fastän funktionen sannerligen inte är noll annat än för just x=0. Om man betraktar denna funktion som en komplexvärd funktion, av en komplex variabel, uppstår inte samma fenomen eftersom funktionen exp(−1/z²) inte går mot 0 då z närmar sig 0 längs den imaginära axeln.

Vissa funktioner kan inte skrivas som Taylorutvecklingr eftersom de har singulariteter. Däremot kan man ofta uttrycka dessa funktioner som potensserier om man godtar negativa potenser av x. Se vidare om Laurentserier.

Parker-Sockackis sats är ett nytt framsteg i försöken att konstruera Taylorutvecklingar som lösningar till differentialekvationer. Denna sats är en utvidgning av Picarditerationen.

Taylorutveckling i flera variabler

Taylorutvecklingar går att generalisera till flera variabler:

$T(x_1,\cdots,x_d) = \sum_{n_1=0}^{\infin} \cdots \sum_{n_d=0}^{\infin} \frac{\partial^{n_1}}{\partial x_1^{n_1}} \cdots \frac{\partial^{n_d}}{\partial x_d^{n_d}} \frac{f(a_1,\cdots,a_d)}{n_1!\cdots n_d!} (x_1-a_1)^{n_1}\cdots (x_d-a_d)^{n_d}$

Till exempel är Taylorutvecklingen till andra ordningen av en funktion av två variabler , x och y i en punkt (a, b):

$f(x,y) \,$

$\approx f(a,b) + f_x(a,b)(x-a) + f_y(a,b)(y-b) \,$

$+ \frac{1}{2}\left( f_{xx}(a,b)(x-a)^2 + 2f_{xy}(a,b)(x-a)(y-b) + f_{yy}(a,b)(y-b)^2 \right).$

En andra ordningens taylorutveckling av en skalär-värd funktion av flera variabler kan skrivas kompakt som

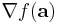$T(\mathbf{x}) = f(\mathbf{a}) + \nabla f(\mathbf{a})^T (\mathbf{x} - \mathbf{a}) + \frac{1}{2} (\mathbf{x} - \mathbf{a})^T \nabla^2 f(\mathbf{a}) (\mathbf{x} - \mathbf{a}) + \cdots$

där $\nabla f(\mathbf{a})$ är gradienten och 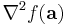$\nabla^2 f(\mathbf{a})$ är Hess-matrisen (icke att förväxla med Laplaceoperatorn verkande på $f$ , som ofta skrivs på detta vis).

Lista över Maclaurinserier

Några viktiga Maclaurinserier följer. Alla dessa gäller även för komplexa variabler x.

Exponentialfunktionen och naturliga logaritmen:

$e^{x} = \sum^{\infin}_{n=0} \frac{x^n}{n!} = 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + \frac{x^4}{24} + \frac{x^5}{120} + \frac{x^6}{720} + \frac{x^7}{5040} + \cdots , \quad \forall x$

$\ln(1+x) = \sum^{\infin}_{n=1} \frac{(-1)^{n+1}}n x^n = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \frac{x^5}{5} - \cdots ,\quad \left| x \right| < 1$

Geometriska serier:

$\frac{1}{1-x} = \sum^{\infin}_{n=0} x^n = 1 + x + x^2 + x^3 + x^4 + x^5 + \cdots,\quad \left| x \right| < 1$

Binomialsatsen:

$(1+x)^\alpha = \sum^{\infin}_{n=0} {\alpha \choose n} x^n,\quad \left| x \right| < 1,\quad\forall \alpha \in C$

Trigonometriska funktioner:

$\sin x = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n+1)!} x^{2n+1} = x - \frac{x^3}{6} + \frac{x^5}{120} - \frac{x^7}{5040} + \cdots,\quad\forall x$

$\cos x = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n)!} x^{2n} = 1 - \frac{x^2}{2} + \frac{x^4}{24} - \frac{x^6}{720} - \cdots ,\quad\forall x$

$\tan x = \sum^{\infin}_{n=1} \frac{B_{2n} (-4)^n (1-4^n)}{(2n)!} x^{2n-1},\quad \left| x \right| < \frac{\pi}{2}$

$\sec x = \sum^{\infin}_{n=0} \frac{(-1)^n E_{2n}}{(2n)!} x^{2n},\quad \left| x \right| < \frac{\pi}{2}$

$\arcsin x = \sum^{\infin}_{n=0} \frac{(2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1}=x+\frac{x^3}{6}+\frac{3x^5}{40} + \frac{5x^7}{112} + \frac{35x^9}{144}+\cdots,\quad \left| x \right| < 1$

$\arctan x = \sum^{\infin}_{n=0} \frac{(-1)^n}{2n+1} x^{2n+1},\quad \left| x \right| < 1$

Hyperboliska funktioner:

$\sinh x = \sum^{\infin}_{n=0} \frac{1}{(2n+1)!} x^{2n+1} = x + \frac{x^3}{6} + \frac{x^5}{120} + \frac{x^7}{5040} + \frac{x^9}{362880} + \cdots,\quad\forall x$

$\cosh x = \sum^{\infin}_{n=0} \frac{1}{(2n)!} x^{2n} = 1 + \frac{x^2}{2} + \frac{x^4}{24} + \frac{x^6}{720} + \frac{x^8}{40320}+\cdots,\quad\forall x$

$\tanh x = \sum^{\infin}_{n=1} \frac{B_{2n} 4^n (4^n-1)}{(2n)!} x^{2n-1},\quad \left| x \right| < \frac{\pi}{2}$

$\sinh^{-1} x = \sum^{\infin}_{n=0} \frac{(-1)^n (2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1},\quad \left| x \right| < 1$

$\tanh^{-1} x = \sum^{\infin}_{n=0} \frac{1}{2n+1} x^{2n+1},\quad \left| x \right| < 1$

Lamberts W-funktion:

$W_0(x) = \sum^{\infin}_{n=1} \frac{(-n)^{n-1}}{n!} x^n = x - x^2 + \frac{x^3}{2} - \frac{x^4}{6} + \frac{x^5}{24} - \cdots,\quad \left| x \right| < \frac{1}{e}$

Talen B_k som dyker upp i uttrycken för tan(x) och tanh(x) är Bernoullital. Binomialutvecklingen använder binomialkoefficienter. E_k i utvecklingen av sec(x) är Eulertal.

Historia

Taylorutvecklingarna, potensserierna, och serieutvecklingarna av funktioner upptäcktes först av den indiske matematikern Madhava på 1300-talet. Han upptäckte en mängd specialfall av Taylorutvecklingarna för de trigonometriska funktionerna sinus, cosinus, tangens samt arcustangens.

På 1600-talet arbetade även matematikern och astronomen James Gregory inom detta område och utgav flera Maclaurinutvecklingar, men det var inte förrän 1715 som Brook Taylor fann den allmänna metoden för att konstruera Taylorutvecklingar för de funktioner som har dem. Maclaurinseriena har namngivits efter den skotske matematikern Colin Maclaurin, som publicerade specialfallet på 1700-talet.

Referenser

F. Eriksson, E. Larsson och G. Wahde, Matematisk analys med tillämpningar, del 3, (1993), Kompendium, Chalmers Tekniska Högskola och Göteborgs Universitet, (Referensen avser endast avsnittet Härledning av Taylorpolynom ovan)