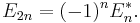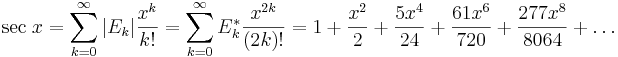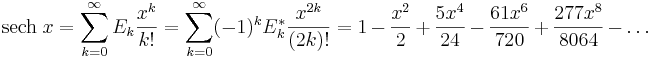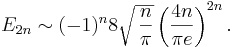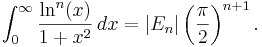Eulertal

Från Rilpedia

Texten från svenska Wikipedia

Eulertalen är heltalssekvens som förekommer i samband med Taylorserier samt i talteori och kombinatorik. Dessvärre finns flera olika konventioner för vad som avses med det n-te Eulertalet: ofta tar man med nollor och negativa tecken i sekvensen, för vilket beteckningen E_n kommer att användas i följande text, medan man i andra tillämpningar bara är intresserad av de nollskilda Eulertalens absolutvärden (här E*_n). Med nämnda beteckningar gäller

E*₁ = 1

E*₂ = 5

E*₃ = 61

E*₄ = 1385

E*₅ = 50521

E*₆ = 2702765

E*₇ = 199360981

E*₈ = 19391512145

E*₉ = 2404879675441

E*₁₀ = 370371188237525

E*₁₁ = 69348874393137901

(talföljd A000364 i OEIS)

E₀ = 1

E₂ = −1

E₄ = 5

E₆ = −61

E₈ = 1385

E₁₀ = −50521

E₁₂ = 2702765

E₁₄ = −199360981

E₁₆ = 19391512145

E_{1, 3, 5, ...} = 0

(talföljd A122045 i OEIS)

och sambandet

$E_{2n} = (-1)^n E_n^*.$

Talen definieras av de genererande funktionerna

$\mathrm{sec}\;x = \sum_{k=0}^\infty | E_k | \frac{x^k}{k!} = \sum_{k=0}^\infty E_k^* \frac{x^{2k}}{(2k)!} = 1 + \frac{x^2}{2} + \frac{5x^4}{24} + \frac{61x^6}{720} + \frac{277x^8}{8064} + \ldots$

$\mathrm{sech}\;x = \sum_{k=0}^\infty E_k \frac{x^k}{k!} = \sum_{k=0}^\infty (-1)^{k} E_{k}^* \frac{x^{2k}}{(2k)!} = 1 - \frac{x^2}{2} + \frac{5x^4}{24} - \frac{61x^6}{720} + \frac{277x^8}{8064} - \ldots$