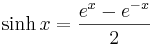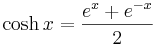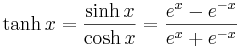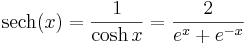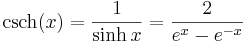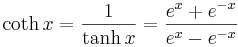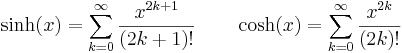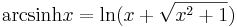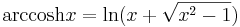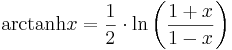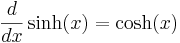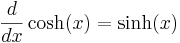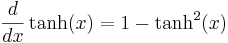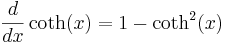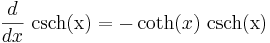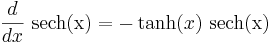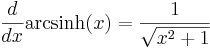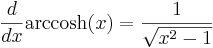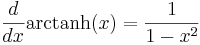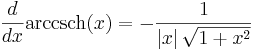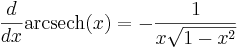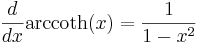Hyperbolisk funktion

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Sinh (röd), cosh (grön) och tanh (blå).

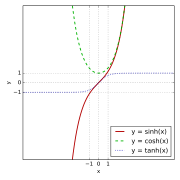
Inom matematiken är de hyperboliska funktionerna nära besläktade med de trigonometriska funktionerna, vilket bland annat märks i deras namn:

  • sinus hyperbolicus (sinh)
  • cosinus hyperbolicus (cosh)
  • tangens hyperbolicus (tanh)
  • secans hyperbolicus (sech)
  • cosecans hyperbolicus (csch)
  • cotangens hyperbolicus (coth)

sech och csch används sällan.

Innehåll

Definition

De hyperboliska funktionerna definieras enligt följande:

  • \sinh x = \frac {e^x - e^{-x}} 2
  • \cosh x = \frac {e^x + e^{-x}} 2
  • \tanh x = \frac {\sinh x}{\cosh x}=\frac{e^x - e^{-x}}{e^x + e^{-x}}
  • \operatorname{sech}(x) = \frac 1 {\cosh x} = \frac 2 {e^x + e^{-x}}
  • \operatorname{csch}(x) = \frac 1 {\sinh x}=\frac 2 {e^x - e^{-x}}
  • \coth x = \frac 1 {\tanh x}=\frac{e^x + e^{-x}}{e^x - e^{-x}}

Om man jämför med Eulers formler, så ser man att definitionen för cosh och cos endast skiljer sig i att man för cos ska multiplicera vinkeln med komplexa enheten i; liknande gäller för sin och sinh. Det gäller att

  • \cosh(x)=\cos(ix), \qquad \cosh(ix)=\cos(x)
  • \sinh(x)=-i\sin(ix), \qquad \sinh(ix) = i\sin(x)

och därmed kan de trigonometriska funktionerna – ur ett analytiskt perspektiv – betraktas som utvidgningar av de hyperboliska funktionerna till det komplexa talplanet. Ur ett geometriskt perspektiv är dock de trigonometriska funktionerna mer grundläggande, och man kan då – ur denna synvinkel – betrakta de hyperboliska funktionerna som utvidgningar till det komplexa talplanet av trigonometriska funktioner.

Taylorserie

Utveckling av de trigonometriska formlerna i en taylorserie görs lätt för sinh och cosh genom att betrakta serieutvecklingen av exponentialfunktionen:

\sinh(x) = \sum_{k=0}^{\infty }\frac{x^{2k+1}}{(2k+1)!} \qquad \cosh(x)=\sum_{k=0}^{\infty }\frac{x^{2k}}{(2k)!}

Identiteter

Motsvarigheten till trigonometriska ettan:

cosh2 x – sinh2 x = 1

sinh är udda, cosh är jämn:

cosh(-x)=cosh x
sinh(-x)=–sinh x

Summor:

  • sinh ( z1 + z2 ) = sinh z1 · cosh z2 + sinh z2 · cosh z1
  • sinh ( z1 – z2 ) = sinh z1 · cosh z2 – sinh z2 · cosh z1
  • cosh ( z1 + z2 ) = cosh z1 · cosh z2 + sinh z1 · sinh z2
  • cosh ( z1 – z2 ) = cosh z1 · cosh z2 – sinh z1 · sinh z2

Inversa funktioner

Liksom de trigonometriska funktionerna har arcus-funktioner som inverser, så benämns med "arcus hyperbolicus" de inversa funktionerna till de hyperboliska funktionerna. Dock kan varje sådan arcus hyperbolicus-funktion skrivas med hjälp av logaritmer:

  • \operatorname{arcsinh} x = \ln(x+\sqrt {x^2+1})
  • \operatorname{arccosh} x = \ln(x+\sqrt {x^2-1})
  • \operatorname{arctanh} x = \frac 1 2\cdot \ln \left( \frac {1+x} {1-x} \right)

Speciellt kan märkas att arcsinh är (entydigt) definierad för hela 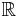\mathbb R till skillnad från inverserna av de trigonometriska funktionerna där man undviker flertydighet genom att införa begreppet principalvärde.

Derivator

\frac{d}{dx}\sinh(x) = \cosh(x) \,
\frac{d}{dx}\cosh(x) = \sinh(x) \,
\frac{d}{dx}\tanh(x) = 1 - \tanh^2(x) \,
\frac{d}{dx}\coth(x) = 1 - \coth^2(x) \,
\frac{d}{dx}\ \hbox{csch(x)} = - \coth(x)\ \hbox{csch(x)}\,
\frac{d}{dx}\ \hbox{sech(x)} = - \tanh(x)\ \hbox{sech(x)}\,
\frac{d}{dx}\operatorname{arcsinh} (x) =\frac{1}{\sqrt{x^{2}+1}}
\frac{d}{dx}\operatorname{arccosh} (x) =\frac{1}{\sqrt{x^{2}-1}}
\frac{d}{dx}\operatorname{arctanh} (x) =\frac{1}{1-x^{2}}
\frac{d}{dx}\operatorname{arccsch} (x) =-\frac{1}{\left| x \right|\sqrt{1+x^{2}}}
\frac{d}{dx}\operatorname{arcsech} (x) =-\frac{1}{x\sqrt{1-x^{2}}}
\frac{d}{dx}\operatorname{arccoth} (x) =\frac{1}{1-x^{2}}

Se även

Externa länkar

  • GonioLab: Visualisering av enhetscirkeln, trigonometriska och hyperboliska funktioner (Java Web Start)
Hämtad från "https://sv.rilpedia.org/wiki/Hyperbolisk_funktion"
Personliga verktyg