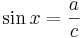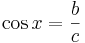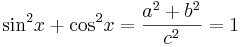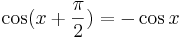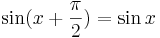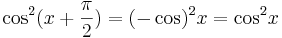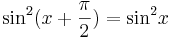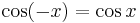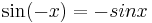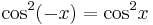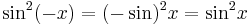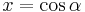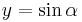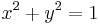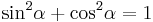Trigonometriska ettan

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Enhetscirkeln

Trigonometriska ettan, ett matematiskt samband som erhålls om Pythagoras sats tillämpas på enhetscirkeln:

\sin^2v+\cos^2v=1 \, .

Innehåll

Bevis

Med rätvinkliga trianglar

I rätvinkliga trianglar har man följade relationer för en vinkel x med närliggande sidor med längda,b och hypotenusan c:

\sin x = \frac{a}{c}
\cos x = \frac{b}{c}

Ur detta får vi att:

{\sin}^2 x + {\cos}^2 x = \frac{a^2 + b^2}{c^2} = 1

Den sista likheten kommer av att a2 + b2 = c2 enligt Pythagoras sats.

Observera att det här endast bevisar satsen för vinklar mellan 0 och 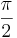\frac{\pi}{2} radianer. För att bevisa satsen för de radianer som uppfyller 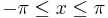-\pi \leq x \leq \pi (det räcker att bevisa för detta intervall då sinus och cosinus är periodiska funktioner), kan man se att:

\cos (x + \frac{\pi}{2}) = -\cos x
\sin (x + \frac{\pi}{2}) = \sin x

Så att:

{\cos}^2 (x + \frac{\pi}{2}) = (-\cos)^2 x = {\cos}^2 x
{\sin}^2 (x + \frac{\pi}{2}) = {\sin}^2 x

Vilket visar att det gäller för 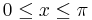0 \leq x \leq \pi . Vi vet då att:

\cos (-x) = \cos x\,
\sin (-x) = -sin x\,

Så att:

{\cos}^2 (-x) = {\cos}^2 x\,
{\sin}^2 (-x) = (-\sin)^2 x = {\sin}^2 x\,

Vilket visar att 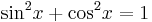{\sin}^2 x + {\cos}^2 x=1\, för intervallet 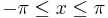-\pi \leq x \leq \pi och därmed för alla x.

Med enhetscirkel

Koordinaterna på enhetscirkeln kan beskrivas med (där α är vinkeln):

x = \cos \alpha\,
y = \sin \alpha\,

Dessa koordinater uppfyller även sambandet (cirkelns ekvation):

x^2 + y^2 = 1 \,

Ur detta följer att:

{\sin}^2 \alpha + {\cos}^2 \alpha = 1\,

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Trigonometriska_ettan"
Personliga verktyg