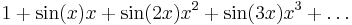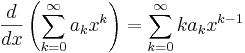Potensserie
Från Rilpedia
En potensserie (i en variabel) är en serie på formen
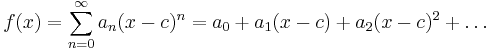
där koefficienterna an, centrumpunkten c och variabeln x vanligtvis är reella eller komplexa tal. Serier av den här typen dyker upp i samband med Taylorserier.
I många sammanhang är c lika med noll, till exempel för en Maclaurinserie. I dessa fall får potensserien det något enklare utseendet
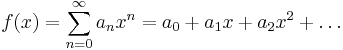
Sådana här potensserier dyker främst upp inom analysen, men också inom kombinatoriken (som genererande funktioner) och elektrotekniken (i Z-transformen). Faktum är att decimalnotationen för heltal kan ses som en potensserie med x fixerad till 10.
Egenskaper
En potensserie 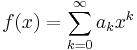 kan för x innanför konvergensradien deriveras och integreras enligt
kan för x innanför konvergensradien deriveras och integreras enligt
Exempel
Ett polynom kan enkelt uttryckas som en potensserie runt något centrum c, även om de flesta koefficienterna blir lika med 0. Till exempel så kan polynomet f(x) = x2 + 2x + 3 skrivas runt c = 0 som
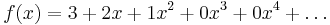
eller runt c = 1 som
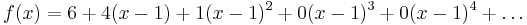
Ett par av de viktigaste exemplen är den geometriska serien
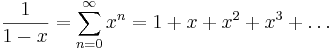
som är giltig för | x | < 1 samt exponentialfunktionen
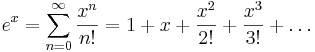
Dessa serier har varit Taylorserier, men det finns potensserier som inte är Taylorserier till någon funktion, till exempel
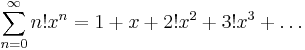
Koefficienterna i en potensserie an får inte bero på x. Följande är alltså inte ett exempel på potensserier