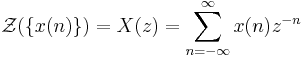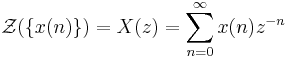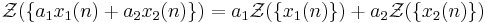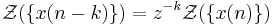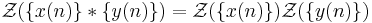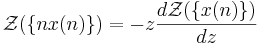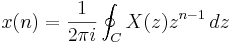Z-transform

Från Rilpedia

Texten från svenska Wikipedia

Z-transformen transformerar en tidsdiskret signal, det vill säga en serie reella tal, till den komplexa frekvensdomänen.

Z-transformen motsvaras i den tidskontinuerliga domänen av Laplace-transformen.

Definition

Z-transformen av en signal $x (n)$ är funktionen $X (z)$ som definieras som

$\mathcal{Z}(\{x(n)\}) = X(z) = \sum_{n=-\infty}^{\infty}x(n)z^{-n}$

där $n$ är ett heltal och $z$ är ett komplext tal.

Om man endast är intresserad av $x (n)$ för icke-negativa värden på $n$ kan man använda följande definition på Z-transformen:

$\mathcal{Z}(\{x(n)\}) = X(z) = \sum_{n=0}^{\infty}x(n)z^{-n}$

Den senare kallas ibland för den enkelsidiga Z-transformen, och den förra för dubbelsidig. Inom signalbehandling används den enkelsidiga då man vet att signalen är kausal.

Egenskaper

Linearitet. Z-transformen av en linjär kombination av två signaler är lika med den linjära kombinationen av de två individuella Z-transformerna.

$\mathcal{Z}(\{a_1 x_1(n) + a_2 x_2(n)\}) = a_1 \mathcal{Z}(\{x_1(n)\}) + a_2 \mathcal{Z}(\{x_2(n)\})$

Tidsförskjutning. Tidsförskjutning av signalen med $k$ steg är detsamma som att multiplicera Z-transformen med $z - k$ .

$\mathcal{Z}(\{x(n-k)\}) = z^{-k}\mathcal{Z}(\{x(n)\})$

Faltning. Z-transformen av faltningen av två sekvenser är produkten av de två individuella Z-transformerna.

$\mathcal{Z}(\{x(n)\}*\{y(n)\}) = \mathcal{Z}(\{x(n)\})\mathcal{Z}(\{y(n)\})$

Derivering.

$\mathcal{Z}(\{nx(n)\}) = -z {{d\mathcal{Z}(\{x(n)\})} \over dz}$

Den inversa Z-transformen kan beräknas som:

$x(n)=\frac{1}{2\pi i}\oint_CX(z)z^{n-1}\,dz$

där $C$ är en sluten kurva kring origo som ligger i $X (z)$ :s konvergensområde.

Den diskreta Fourier-transformen är ett specialfall av Z-transformen med $z = e j ω$ .

Z-transform

Från Rilpedia

Definition

Egenskaper

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk