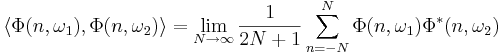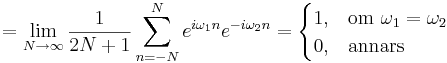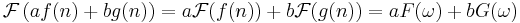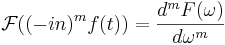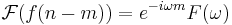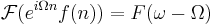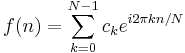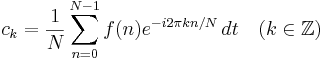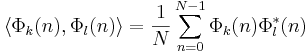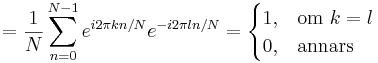Fouriertransform
Från Rilpedia
Fouriertransformen, efter Jean Baptiste Joseph Fourier, är en transform som överför en funktion från tidsplanet till frekvensplanet. Där uttrycks funktionen som summan av sina sinusoidala basfunktioner, eller deltoner. Dessa är sinsemellan ortogonala, vilket gör transformering till och från frekvensplanet relativt enkla.
Fouriertransfomen har stor betydelse inom alla områden där frekvensanalys är av intresse. Den kan även användas för att underlätta lösning av differentialekvationer.
Fouriertransformen är definierad för såväl tidskontinuerliga som tidsdiskreta signaler. När den används på tidsbegränsade eller periodiska signaler benämns resultatet normalt Fourierserier.
Innehåll |
Definitioner
Tidskontinuerlig Fouriertransform
Fouriertransformen för en reell- eller komplexvärd funktion 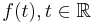 , definieras som:
, definieras som:
Motsvarande inverstransform:
Basfunktionerna är:
De är ortogonala:
Den tidskontinuerliga Fouriertransformen är en variant av Laplacetransformen, med parametern s = iω. Egenskaper för Fouriertransformen är:
- Tids- och frekvensförskjutning
Tidskontinuerlig Fourierserie
Fourier-serien för en reell- eller komplexvärd tidsbegränsad funktion 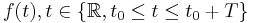 , eller för en reell- eller komplexvärd periodisk funktion f(t) med periodiciteten T, definieras som:
, eller för en reell- eller komplexvärd periodisk funktion f(t) med periodiciteten T, definieras som:
där
Basfunktionerna är:
- Φk(t) = ei2πkt / T
De är ortogonala:
Tidsdiskret Fouriertransform
Fouriertransformen för en reell- eller komplexvärd funktion 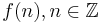 , definieras som:
, definieras som:
Motsvarande inverstransform:
Basfunktionerna är:
De är ortogonala:
Den tidsdiskreta Fouriertransformen är en variant av Z-transformen, med parametern z = eiω. Egenskaper för Fouriertransformen är:
- Linearitet
- Derivering
- Faltning och multiplikation
-
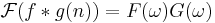
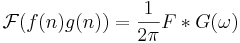 (cyklisk faltning över 2π)
(cyklisk faltning över 2π)
- Tids- och frekvensförskjutning
Φ(n,ω) (och därmed F(ω)) är en periodisk funktion med periodiciteten 2π.
Tidsdiskret Fourierserie
Fouriertransformen för en reell- eller komplexvärd funktion 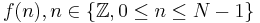 , definieras som:
, definieras som:
där
Basfunktionerna är:
- Φk(n) = ei2πkn / N
De är ortogonala:
Den tidsdiskreta Fourierserien kräver i allmänhet N2 komplexa multiplikationer. Algoritmer för att beräkna den betydligt snabbare går under namnet FFT (Fast Fourier Transform), vilka kräver i storleksordningen NlogN komplexa multiplikationer.




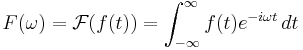
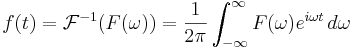
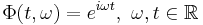
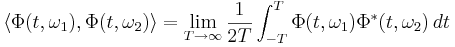
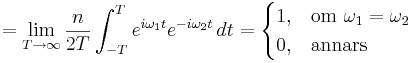
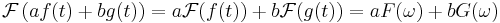
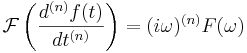
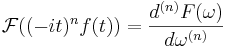
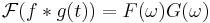
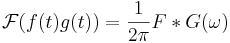
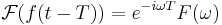
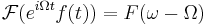
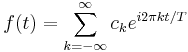
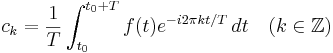
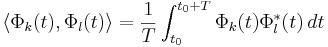
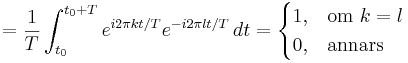
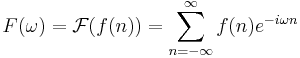
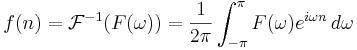
![\Phi(n,\omega) = e^{i\omega n},\quad \omega\in\{\mathbb{R}:\,[-\pi,\pi]\}](/w/images/sv.rilpedia.org/math/e/8/8/e881fd3963698747944e830dbf72b12b.png)