Fourierserie
Från Rilpedia

Fourierserier, efter Jean Baptiste Joseph Fourier, är en variant av Fouriertransformen för funktioner som bara är definierade för ett intervall av längden T, eller som är periodiska med periodiciteten T. Varje kontinuerlig periodisk funktion kan skrivas som summan av ett antal sinusfunktioner med varierande amplitud där varje sinusfunktion har en frekvens som är en heltalsmultipel av den lägsta frekvensen i den periodiska funktionen, 1/T (grundtonen).
Fourierutvecklingen av en funktion f med perioden 2π kan definieras som
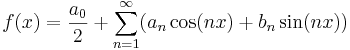 , där
, där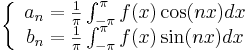
Inte alla periodiska funktioner kan skrivas som en Fourier-serie där serien konvergerar punktvis. Ett tillräckligt villkor är t ex att f är deriverbar.
Mer allmänt kan Fourierutvecklingen av en vektor 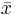 relativt en ortonormerad bas
relativt en ortonormerad bas 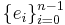 i ett Hilbertrum definieras som
i ett Hilbertrum definieras som
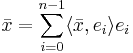 , för någon inre produkt
, för någon inre produkt 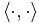 .
.
Se även
 Wikimedia Commons har media som rör Fourierserie
Wikimedia Commons har media som rör Fourierserie
- Delton
- Snabb Fouriertransform (FFT)



