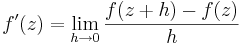Analytisk funktion
Från Rilpedia
Analytiska funktioner (även komplexanalytiska funktioner eller holomorfa funktioner) studerar man i den del av matematiken som kallas komplex analys.
En komplexvärd funktion f av en komplex variabel z är analytisk i punkten z0 om dess komplexa derivata
existerar för alla z i en omgivning av z0, där h är ett komplext tal, vilket kan tyckas vara en obetydlig förändring jämfört med definitionen på reellvärd derivata, men innebär en mycket annorlunda teori jämfört med reell analys. Den är analytisk i ett område Ω i komplexa planet om den är analytisk i varje punkt z i Ω. En funktion som är analytisk i hela komplexa planet kallas hel funktion.
Exempel på hela funktioner är
- polynomfunktioner,
- f(z) = ez,
- f(z) = sin(z).
Exempel på kontinuerliga funktioner som inte är analytiska i någon punkt är
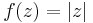 ,
,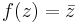 (komplexkonjugatet av z).
(komplexkonjugatet av z).
Enligt en sats ur komplexa anlysen har varje analytisk funktion också analytisk derivata. Det medför att om en funktion har en derivata har den oändligt många derivator och kan utvecklas i potensserie. Löst uttryckt innebär detta att analytiska funktioner med nödvändighet "uppför sig väl". Jämför med det reella fallet där även om en funktion är deriverbar behöver inte högre ordningars derivator existera.
Varje analytisk funktion uppfyller Cauchy-Riemanns ekvationer.
De enda hela begränsade funktionerna är enligt Liouvilles sats de konstanta funktionerna. Detta leder till ett koncist bevis för den viktiga algebrans fundamentalsats.
Analytiska funktioner uppfyller Cauchys integralsats. Genom att betrakta "nästan" analytiska funktioner kan man visa Cauchys integralformel som är ett kraftfullt verktyg för beräkning av vissa integraler (exempelvis Fouriertransformen) som är svåråtkomliga med andra metoder. Teorin har även kopplingar till icke-euklidisk geometri, särskilt via Möbiusavbildningar och konforma avbildningar.
En teoretiskt mycket viktig egenskap, och ett av de elegantaste resultaten i hela teorin för analytiska funktioner av en komplex variabel, ges av Riemanns avbildningssats som innebär att varje öppen enkelt sammanhängande mängd, skild från hela komplexa talplanet 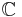 kan avbildas konformt till det inre av enhetscirkeln. Det betyder till exempel att man i princip alltid kan lösa Laplaces ekvation i
kan avbildas konformt till det inre av enhetscirkeln. Det betyder till exempel att man i princip alltid kan lösa Laplaces ekvation i 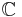 och
och 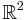 .
.
I modern forskning studerar man även komplex analys i flera variabler, där teorin skiljer sig åt betydligt jämfört med komplex analys i en variabel.