Icke-euklidisk geometri
Från Rilpedia
I en icke-euklidisk geometri gäller inte Euklides femte axiom, det så kallade parallellaxiomet. (Väljer man att godta parallellaxiomet får man euklidisk geometri.)
Termen icke-euklidisk geometri beskriver både hyperbolisk och elliptisk geometri, som står i kontrast till euklidisk geometri. Den väsentliga skillnaden mellan euklidisk och icke-euklidisk geometri är de parallella linjernas natur. I euklidisk geometri, om vi startar i en punkt A och en linje l, så kan vi endast dra en linje genom A som är parallell med l. Å andra sidan, i hyperbolisk geometri finns det oändligt många linjer genom A parallella med l, och i elliptisk geometri existerar inte parallella linjer. (Se hyperbolisk geometri och elliptisk geometri för ytterligare information.)
Ett annat sätt att beskriva skillnaderna mellan dessa geometrier är som följande: betrakta två linjer i ett plan som båda är vinkelräta mot en tredje linje. I euklidisk och hyperbolisk geometri är då de två linjerna parallella. I euklidisk geometri förblir emellertid de två linjerna på ett konstant avstånd, medan i hyperbolisk geometri "böjer de av" från varandra med ökande avstånd i takt med att avståndet från skärningspunkten med den gemensamma vinkelräta linjen ökar. I elliptisk geometri "kröker" linjerna mot varandra, och slutligen skär de varandra; således existerar inga parallella linjer i elliptisk geometri.
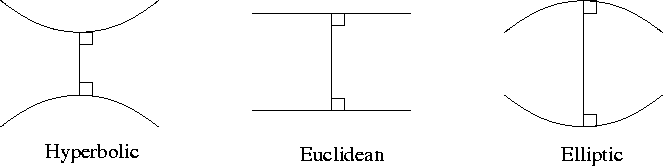
Beteende hos linjer med gemensam ortogonal linje i vardera av de tre sorternas geometri
Innehåll |
Historik
Medan euklidisk geometri (namngiven efter den grekiske matematikern Euklides) inkluderar några av de äldsta kända matematiska teoremen, så dröjde det ända till 1800-talet innan icke-euklidisk geometris legitimitet blev allmänt accepterad. Debatten som slutligen ledde till upptäckandet av icke-euklidiska geometrier började nästan så snart Euklides' verk Elementa var klart. I Elementa försöker Euklides etablera en fullständigt logisk bas för matematiken känd vid hans era. Hans arbete började med ett begränsat antal antaganden (kallade axiom och postulat) och försökte bevisa alla andra resultat (teorem) i hans arbete. Det mest välbekanta postulatet kallas ofta Euklides femte postulat, eller helt enkelt "parallellpostulatet", som i Euklides originalformulering är:
- "Om en rät linje skär två räta linjer på så sätt att de inre vinklarna på samma sida tillsammans är mindre än två räta vinklar, så möts de räta linjerna, om de förlängs i oändlighet, på den sida där vinklarna är mindre än de två räta vinklarna."
Enklare formuleringar av detta postulat har skrivits (se artikeln om parallellpostulat för några exempel på ekvivalenta påståenden). Oavsett hur det formuleras, tycks det alltid vara mer komplicerat än Euklides övriga postulat (som till exempel inkluderar, "Mellan valfria två punkter kan en rät linje dras").
Under flera hundra år var geometriker bekymrade över den det femte postulatets speciella komplexitet, och trodde att det kunde bevisas som ett teorem ur de övriga fyra. Många försökte finna ett bevis genom motsägelse, i synnerhet Italienaren Giovanni Gerolamo Saccheri. I ett arbete med titeln Euclides ab Omnio Naevo Vindicatus (Euklides befriad från alla brister), publicerad 1733, förkastade han snabbt elliptisk geometri som en möjlighet (några andra av Euklides axiom måste modifieras för att elliptisk geometri ska fungera) och satte igång att bevisa ett stort antal resultat i hyperbolisk geometri. Till slut nådde han en punkt där han trodde att hans resultat visade på motsägelser i systemet, och därmed bevisade att hyperbolisk geometri är ologisk. Hans hävdande om motsägelse tycks grundas på euklidiska antaganden, därför att någon motsägelse fanns inte i hans eget verk.
Cirka hundra år senare, 1829, publicerade den ryska matematikern Nikolaj Lobatjevskij en avhandling om hyperbolisk geometri. Därför kallas hyperbolisk geometri ibland för Lobatjevskijsk geometri. Vid samma tid skrev även ungraren Janos Bolyai en avhandling om hyperbolisk geometri, som publicerades 1832 som ett appendix till ett verk av dennes far. Den store matematikern Carl Friedrich Gauss läste appendixet och avslöjade för Bolyai att han själv hade utarbetat samma resultat någon gång tidigare. Den fundamentala skillnaden mellan dessa och tidigare arbeten, som Saccheris, är att de var de första att öppet hävda att euklidisk geometri inte var den enda geometrin, och inte heller den enda möjliga geometriska strukturen för universum. Dock återstod ännu möjligheten att axiomen för hyperbolisk geometri var logiskt självmotsägande.
Det behövdes dock mera arbete för att etablera elliptisk geometri. Bernhard Riemann grundlade under en berömd föreläsning 1854 fältet riemanngeometri, som särskilt diskuterade idéerna som nu kallas "mångfalder", riemannmetrik och krökning. Han konstruerade en oändlig familj av icke-euklidiska geometrier genom att ge en formel för en familj av riemannmetriker på enhetsklotet i euklidiska rum. Ibland förbises delar av hans upptäckter, men hans konstruktioner visar att hans arbete var långtgående, hans teorem är giltiga för alla geometrier.
Euklidisk geometri modelleras genom vårt begrepp om ett "platt plan". Den enklaste modellen för elliptisk geometri är en sfär, där linjer är "storcirklar" (som ekvatorn eller meridianer på en jordglob). Även efter Lobatjevskijs, Gauss, och Bolyais arbeten återstod frågan: existerar någon sådan modell för hyperbolisk geometri? Denna fråga besvarades av Eugenio Beltrami 1864, som bevisade att en yta kallad pseudosfär har den lämpliga krökningen för att modellera hyperbolisk geometri. Hans arbete byggde direkt på Riemanns. Betydelsen av Beltramis arbete ligger i att han visade att hyperbolisk geometri är logiskt motsägelsefri om euklidisk geometri är det.
Utvecklingen av icke-euklidisk geometri visade sig vara mycket viktig för fysik på 1900-talet. Einsteins Relativitetsteori beskriver rummet som allmänt platt (d.v.s. euklidiskt), men krökt (d.v.s. icke-euklidiskt) i regioner nära materia. Denna typ av geometri, där krökningen ändras från punkt till punkt, kallas pseudo-euklidisk geometri.
Referenser
- http://www.wikipedia.org/wiki/Non-euclidean_geometry
- Ian Stewart; Flatterland; Perseus Publishing; ISBN 0-7382-0675-X (softcover, 2001)



