Från Rilpedia

En pseudosfär är en trumpetformad rotationsyta, som kan beskrivas med en matematisk graf, liksom kuben, sfären mm.

Man kan visa att pseudosfären har konstant Gausskrökning -1. Namnet "pseudosfär" används därför för att den är en tvådimensionell yta med konstant krökning. Precis som sfären i varje punkt har den positivt krökta geometrin hos ett kupolvalv, så har hela pseudosfären i varja punkt den negativt krökta ytan hos en sadel.

Pseudosfären uppkommer genom att rotera en traktriskurva till en linje 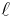i planet kring denna linje. Traktrisen kan karakteriseras på följande vis. Betrakta det segment av tangentlinjen till kurvan vars ändpunkter är tangeringspunkten (med kurvan) samt skärningspunkten med 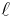. Längden av detta segment är lika med 1 för varje punkt på traktrisen.

En parametrisering av en psuedosfär ges av

I detta fall ligger kurvan i xz-planet, och rotationslinjen ges av z-axeln.

Referens

• Henderson, D. W. och Taimina, D.; Aesthetics and Mathematics, Springer-Verlag (2006)Experiencing Geometry: Euclidean and Non-Euclidean with History

Externa länkar

• http://www.geom.uiuc.edu/zoo/diffgeom/pseudosphere/
• Funktionen uttryckt som ekvation: http://www.geom.uiuc.edu/zoo/diffgeom/pseudosphere/eqns.html