Algebrans fundamentalsats

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Algebrans fundamentalsats kan uttryckas som:

Ett polynom 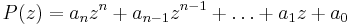$P(z) = a_nz^n + a_{n-1}z^{n-1} + \ldots + a_1z + a_0$ av graden $n > 0$ med komplexa koefficienter $a_0 \ldots a_n$ har minst en komplex rot.

Ett annat sätt att uttrycka detta är: Varje algebraisk ekvation med komplexa koefficienter av graden $n$ , där $n$ är större än 1, har precis $n$ komplexa nollställen, räknade med multiplicitet (det vill säga, några rötter kan vara lika). Detta kan tyckas vara ett betydligt starkare resultat, men kan i själva verket lätt visas vara ekvivalent med det första påståendet, genom användning av faktorsatsen.

Observera att det anges att koefficienterna är komplexa tal, men det innefattar även de reella talen, eftersom dessa är komplexa tal med en imaginärdel som är noll.

Exempel

En andragradsekvation

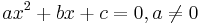
$ax^2 + bx + c = 0, a\neq 0$

har alltid två rötter. Dessa är

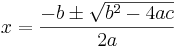
$x = {-b \pm \sqrt{b^2-4ac} \over 2a}$

Om uttrycket under rottecknet är

större än noll, är rötterna olika och reella
mindre än noll, är rötterna olika och icke-reella
lika med noll, är rötterna lika och reella

Ett komplexanalytiskt bevis

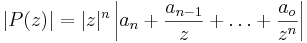
$|P(z)| = |z|^n \left| a_n + \frac{a_{n-1}}{z} + \ldots + \frac{a_o}{z^n} \right|$

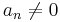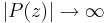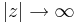Där $a_n \neq 0$ . Nu ser vi att $|P(z)| \to \infty$ då $|z| \to \infty$ .

Antag att $P (z)$ saknar nollställen. Då är funktionen 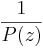$\frac{1}{P(z)}$ en hel analytisk funktion. Eftersom den har gränsvärdet 0 då absolutbeloppet av $z$ går mot oändligheten är den begränsad i hela komplexa talplanet. Enligt Liouvilles sats är därför 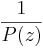$\frac{1}{P(z)}$ konstant. Men då är även $P (z)$ konstant, vilket är en motsägelse då $n > 0$ . Följaktligen har $P (z)$ minst ett komplext nollställe.

Algebraiska bevis

Satsen kan också visas med mer algebraiska metoder. På grund av den topologiska naturen i konstruktionen av reella, och därmed komplexa, tal kan man emellertid inte helt undvika topologiska metoder. Man kan emellertid visa, med hjälp av bland annat galoisteori att en utvidning av grad 2 av en reellt sluten kropp är algebraiskt sluten. Därmed följer algebrans fundamentalsats om man kan visa att de reella talen är reellt slutna. Detta svarar mot att uddagradspolynom alltid har lösningar, någon som kan visas med hjälp av satsen om mellanliggande värden

Se även

Algebrans fundamentalsats

Från Rilpedia

Innehåll

Exempel

Ett komplexanalytiskt bevis

Algebraiska bevis

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk