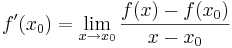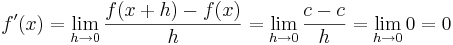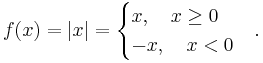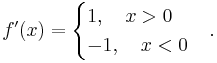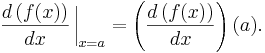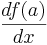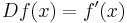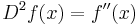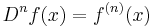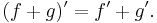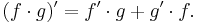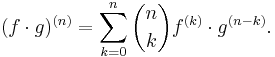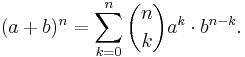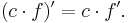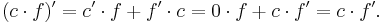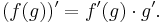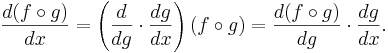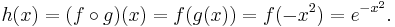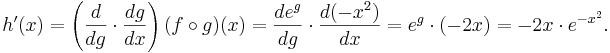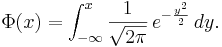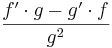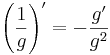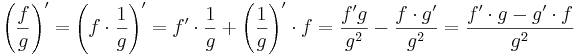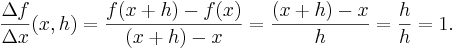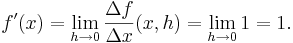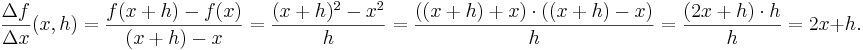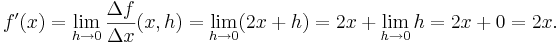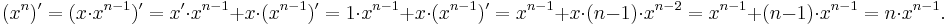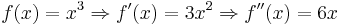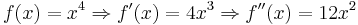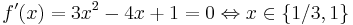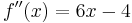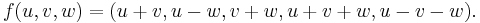Derivata
Från Rilpedia

Inom matematik är derivatan en funktion som anger hur en annan, känd funktion förändras beroende på vilken indata funktionen får, funktionens förändringshastighet. Intuitivt kan en funktions derivata sägas beskriva hur mycket och i vilken riktning en funktions värde förändras om man rör sig från en given punkt. Exempelvis kan positionen för en bil i rörelse beskrivas som en funktion av tiden som har passerat sedan bilen sattes i rörelse, derivatan av denna funktion beskriver bilens hastighet (hur mycket läget för bilen förändras inom den närmaste framtiden) och derivatan av derivatan är bilens acceleration (hur mycket hastigheten förändras).
Derivata är ett grundläggande begrepp inom matematisk analys. Den enklaste formen av derivata är derivatan av en reellvärd funktion av en reell oberoende variabel, där derivatan är den hastighet med vilken funktionsvärdet ändras i den punkt som svarar mot den oberoende variabelns värde. Då förändringshastigheten hos en funktion inte måste vara konstant med avseende på den oberoende variabeln, är även derivatan en funktion av denna.
För en reellvärd funktion f av en variabel betecknas derivatan vanligen f ′, varför derivatan i punkten x följaktligen betecknas f ′(x) (uttalas "f-prim av x".). Derivatan kan också betecknas df/dx (uttalas "d-f, d-x").
Innehåll |
Exempel
Exempel 1:
- Antag att p(h) betyder lufttrycket (i pascal) vid höjden h (i meter) över havsnivån. Då kommer derivatan p′(h) att ange hur mycket trycket ökar per meter i höjdled. Derivatan får alltså den fysikaliska enheten pascal per meter. Eftersom trycket i själva verket avtar med höjden, kommer alltså derivatan att bli negativ.
Exempel 2:
- Låt f vara en konstant funktion definierad av f(x) = c. Då blir derivatan f ′(x) = 0 för alla x, eftersom funktionens värde inte ändras alls när x ändras.
Definition
Derivatan av funktionen f i punkten x0 definieras som gränsvärdet
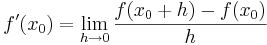 ,
,
Om gränsvärdet existerar i en viss punkt sägs funktionen vara deriverbar i punkten. Om funktionen är deriverbar i varje punkt i definitionsmängden sägs funktionen vara deriverbar. Om funktionen endast är deriverbar i vissa intervall, måste intervallen anges som villkor för deriverbarheten.
Det finns även en omskrivning av gränsvärdet, vilken kan vara användbar vid bevisföring:
Exempel
Derivatan av den konstanta funktionen, 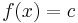 , sades tidigare vara lika med noll eftersom den inte förändras då variabeln ändras. Med derivatans definition går det att visa detta mer stringent:
, sades tidigare vara lika med noll eftersom den inte förändras då variabeln ändras. Med derivatans definition går det att visa detta mer stringent:
Geometrisk tolkning
Om en funktion f åskådliggörs av en graf y = f(x) så anger derivatan av f grafens lutning (förändring i y per förändring i x) för varje värde x. Derivatan i en punkt är således lika med riktningskoefficienten för kurvans tangent i den valda punkten (x, f(x)). Tangentens lutning kan approximeras med sekantens lutning i ett litet område kring punkten x. Om sekanten går genom punkterna (x, f(x)) och (x+h, f(x+h)), där h är ett litet tal, blir dess lutning (och funktionens medellutning) i detta intervall lika med
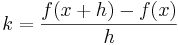 .
.
Approximationen blir bättre ju mindre h väljs; om avståndet h mellan punkternas x-värden går mot noll, så kommer sekanten att övergå till tangenten vid x och lutningen kommer att gå mot derivatan f ′(x); härav derivatans definition.
Det finns ett teorem som säger att om en funktion är deriverbar i en punkt, så är den även kontinuerlig i denna punkt. Det motsatta förhållandet behöver inte gälla, vilket visas av bland annat Weierstrass exempel. Ett enklare exempel än Weierstrass ges av absolutbelopps-funktionen:
Detta är en kontinuerlig funktion som är deriverbar för varje tal x, med undantag av talet noll:
Funktionens derivata är odefinierad för talet noll. Däremot har funktionen en höger- och en vänsterderivata för talet noll: Högerderivatan i noll är talet +1 och vänsterderivatan i noll är talet -1. Om däremot höger- och vänsterderivatan i en punkt existerar och har samma värde så existerar även derivatan i denna punkt.
Högre ordningars derivator
Om man beräknar derivatan av en funktions derivata erhåller man en andra ordningens derivata', även kallad andraderivata. Beräknar man derivatan av denna får man tredjederivatan och så vidare. Om risk för förväxling föreligger kallas derivatan av ursprungsfunktionen förstaderivata.
Notation
Som tidigare nämnts finns ett flertal olika notationer för derivata. Med undantag av Newtons notation innebär dessa vanligen ingen skillnad i natur. Olika områden inom matematiken har dock vanligen en notation som vanligen används.
Lagranges notation
Den enklaste varianten som används är Joseph Louis Lagranges, nämligen primtecknet:
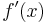 för förstaderivata (uttalas "f-prim av x")
för förstaderivata (uttalas "f-prim av x")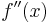 för andraderivata (uttalas "f-bis av x")
för andraderivata (uttalas "f-bis av x")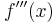 för tredjederivata (uttalas "f-tris av x")
för tredjederivata (uttalas "f-tris av x")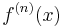 för högre ordningens derivata, eller derivator av okänd ordning (som i exempelvis Taylorutvecklingar).
för högre ordningens derivata, eller derivator av okänd ordning (som i exempelvis Taylorutvecklingar).
Leibniz notation
Den andra typen av notation har fått sitt namn efter Gottfried Leibniz. Även om den kan tyckas något otymplig är den lämplig att använda bland annat vid tillämpning av kedjeregeln och vid lösning av differentialekvationer, på grund av dess tydliggörande av differentialerna.
För derivatan av en funktion 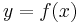 skriver man
skriver man
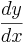 eller
eller 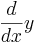 för förstaderivatan och
för förstaderivatan och 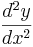 eller
eller 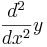 för andraderivatan.
för andraderivatan.
Om sammanhanget gör det lämpligare att använda 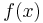 i stället för
i stället för 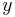 skriver man
skriver man
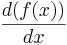 (eller
(eller 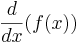 ) i stället för
) i stället för 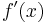 ,
, 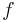 :s derivata.
:s derivata.
För f:s derivata i en punkt a finns två notationer:
Ibland skrivs detta dock något slarvigt som
Högre ordningens derivator skrivs som
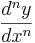 eller
eller 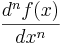 i stället för
i stället för 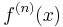 .
.
Newtons notation
Isaac Newtons notation använder en punkt över funktionen för att beteckna derivata. Den används idag främst inom mekanik för att beteckna derivator med avseende på tiden, för att särskilja dessa från derivator med avseende på rummet. Den används vanligen endast för första och andra ordningens derivator:
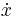 för förstaderivatan (uttalas "x-prick")
för förstaderivatan (uttalas "x-prick")
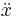 för andraderivatan (uttalas "x-prick-prick")
för andraderivatan (uttalas "x-prick-prick")
Då Leibniz notation är mer användarvänlig föredras vanligtvis denna framför Newtons notation
Eulers notation
Leonhard Euler introducerade en notation baserad på en differentieringsoperator:
Deriveringsregler
Vid derivering är det oftast onödigt komplicerat att utgå från derivatans definition; istället har man utifrån definitionen härlett derivatorna till de elementära funktionerna och uttryck sammansatta av sådana. Dessa kan man utgå från vid problemlösning.
Många funktioner kan skrivas på endera av följande sätt:
- Som en summa av två funktioner, exempelvis
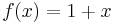 ;
; - som en produkt av två funktioner, exempelvis
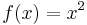 ;
; - som en kvot av två funktioner, exempelvis
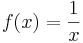 ;
; - som en sammansättning av två funktioner; så är exempelvis funktionen
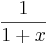 en sammansättning av funktionerna
en sammansättning av funktionerna 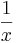 och
och 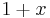 .
.
För att beräkna derivatorna av sådana funktioner använder man någon av följande regler.
Additionsregeln
Derivatan av en summa av två funktioner som båda är deriverbara:
Produktregeln
Produkten av två deriverbara funktioner är deriverbar, och derivatan ges av följande formel.
Produkten av två n gånger deriverbara funktioner är också n gånger deriverbar; den n:te derivatan ges av följande formel som är uppkallad efter den tyske matematikern Gottfried Wilhelm von Leibniz.
Anmärkning
Jämför med Binomialsatsens utveckling av ett binom (a + b)n.
Om man formellt skriver 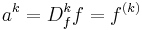 och
och 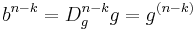 så kan Leibniz formel skrivas på följande sätt.
så kan Leibniz formel skrivas på följande sätt.
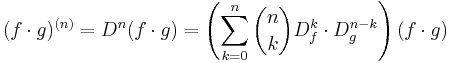 .
.
Deriveringsoperatorn D uppfyller tydligen följande samband.
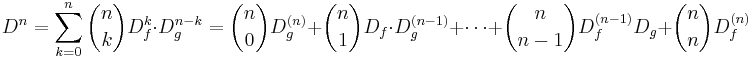 .
.
Linjäritet
En konstant (c) kan flyttas ut ur deriveringen:
Bevis
Tillämpa produktregeln på funktionen 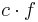 , där c är ett fixerat tal (det vill säga en konstant funktion), och kommer ihåg att derivatan av en konstant funktion är lika med noll:
, där c är ett fixerat tal (det vill säga en konstant funktion), och kommer ihåg att derivatan av en konstant funktion är lika med noll:
Derivata av sammansatt funktion (kedjeregeln)
En sammansatt funktion f(g(x)) är en funktion f(x) som har en annan funktion g(x) som sitt argument, istället för en variabel som x. Detta kan även skrivas 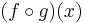 för att förtydliga att g inte är en variabel utan själv är en funktion av variabeln x. Derivatan av en sammansatt funktion går under namnet kedjeregeln:
för att förtydliga att g inte är en variabel utan själv är en funktion av variabeln x. Derivatan av en sammansatt funktion går under namnet kedjeregeln:
Ett tydligare sätt att framställa kedjeregeln är att använda Leibniz notation:
Exempel
Funktionen 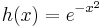 är sammansatt av funktionerna
är sammansatt av funktionerna 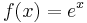 och
och 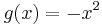 :
:
Dess derivata kan beräknas med hjälp av kedjeregeln:
Av detta kan vi bland andra dra följande slutsatser: Om talet x är negativt så är funktionen h växande (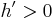 ); om talet x är positivt är funktionen h avtagande (
); om talet x är positivt är funktionen h avtagande (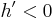 ).
).
Inom sannolikhetsteori och statistik är denna funktion av stor betydelse då den utgör fördelningsfunktionen för den så kallade normalfördelningen:
Dess betydelse härrör från den berömda Centrala gränsvärdessatsen.
Kvotregeln
I de punkter där funktionen g inte är lika med noll, och där den har en derivata, är derivatan av kvoten f/g följande funktion:
Bevis
Börja med att beräkna derivatan av funktionen 1/g används derivatan av en sammansatt funktion, och vetskapen att derivatan av 1/x är -1/x2, vilket ger att
Nu går det att använda produktregeln för att räkna ut derivatan av f(x)/g(x):
Derivata av invers
Anta att 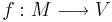 är en funktion som är inverterbar och som har en derivata som inte är lika med noll. Då är funktionens invers
är en funktion som är inverterbar och som har en derivata som inte är lika med noll. Då är funktionens invers 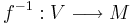 också deriverbar, och dess derivata ges av följande formel.
också deriverbar, och dess derivata ges av följande formel.
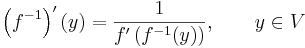 .
.
Exempel
Funktionen 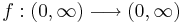 med f(x) = x2, är inverterbar och dess invers är funktionen
med f(x) = x2, är inverterbar och dess invers är funktionen 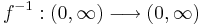 med
med 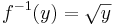 . Inversens derivata kan beräknas med formeln ovan.
. Inversens derivata kan beräknas med formeln ovan.
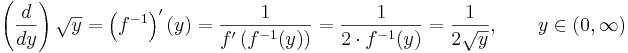 .
.
De elementära funktionernas derivator
Derivata av polynomfunktioner
Polynomfunktion av grad ett
Derivatan av funktionen 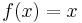 är funktionen
är funktionen 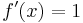 .
.
-
- Eftersom differenskvoten alltid är lika med talet ett, kommer dess gränsvärde också att vara lika med talet ett:
Polynomfunktion av grad två
Genom att tillämpa den så kallade konjugatregeln kan vi beräkna derivatan av polynomfunktionen 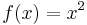 .
.
- Först skall vi bearbeta funktionens differenskvot i en godtyckligt vald punkt (x) i funktionens definitionsmängd:
- Då talet h närmar sig talet noll, närmar sig differenskvoten polynomfunktionens derivata
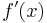 i punkten x:
i punkten x:
Polynomfunktion av godtycklig grad
Om vi skriver talet ett som 1 = x0, så kan vi se ett mönster mellan funktionerna och deras derivator: Funktionen f(x) = x2 har derivatan 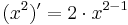 ; funktionen f(x) = x1 har derivatan
; funktionen f(x) = x1 har derivatan 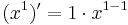 ; funktionen f(x) = x0 har derivatan
; funktionen f(x) = x0 har derivatan 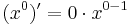 . Vi kan därför misstänka att om n är ett positivt heltal så har funktionen f(x) = xn derivatan
. Vi kan därför misstänka att om n är ett positivt heltal så har funktionen f(x) = xn derivatan 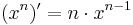 .
.
Vi vet att vår hypotes stämmer då n = 0, 1 och 2. Med hjälp av produktregeln (se denna artikel) skall vi visa att hypotesen är helt korrekt för samtliga heltal n.
Säg att vi vet att derivatan av funktionen 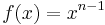 är funktionen
är funktionen 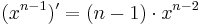 , där n är ett visst positivt heltal (exempelvis talet 2). Om vi skriver funktionen
, där n är ett visst positivt heltal (exempelvis talet 2). Om vi skriver funktionen 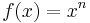 som en produkt av funktionerna x och xn − 1 så säger produktregeln att derivatan av funktionen xn är följande funktion:
som en produkt av funktionerna x och xn − 1 så säger produktregeln att derivatan av funktionen xn är följande funktion:
Denna beräkning visar att om vi vet hur derivatan av funktionen x2 ser ut, så vet vi hur derivatan av funktionen x3 ser ut; och om vi vet hur derivatan av funktionen x3 ser ut så vet vi hur derivatan av funktionen x4 ser ut, och så vidare.
Tabeller över elementära funktioner och deras derivator
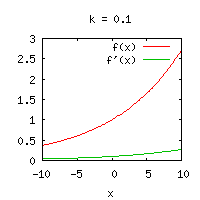
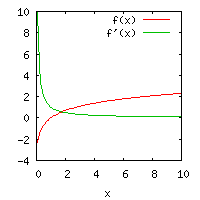
Derivator av exponential- och potensfunktioner
| Funktion | Derivata | Grafer för funktion och derivata |
|---|---|---|
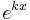 |
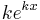 |
 |
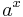 |
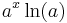 |
 |
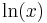 |
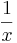 |
 |
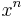 |
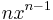 |
 |
De trigonometriska och hyperboliska funktionerna påminner på flera sätt starkt om varandra, vilket även avspeglar sig i deras derivator:
| De trigonometriska funktionerna | De hyperboliska funktionerna | ||
|---|---|---|---|
| Funktion | Derivata | Funktion | Derivata |
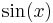 |
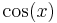 |
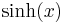 |
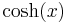 |
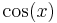 |
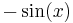 |
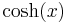 |
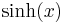 |
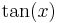 |
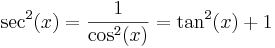 |
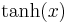 |
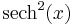 |
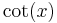 |
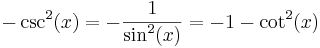 |
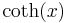 |
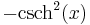 |
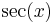 |
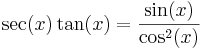 |
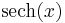 |
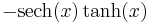 |
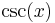 |
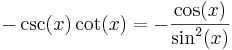 |
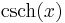 |
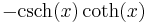 |
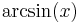 |
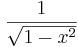 |
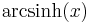 |
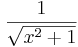 |
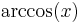 |
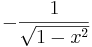 |
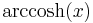 |
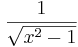 |
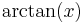 |
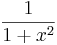 |
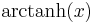 |
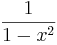 |
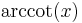 |
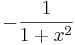 |
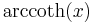 |
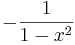 |
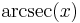 |
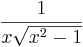 |
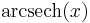 |
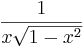 |
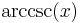 |
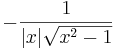 |
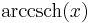 |
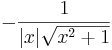 |
Tillämpningar
Derivator utnyttjas allmänt i flera områden inom matematik och fysik, men även andra vetenskaper utnyttjar dem mer eller mindre flitigt.
Kritiska punkter
Det är klart från definitionen av derivata att en funktion växer (dess graf stiger) när derivatan är positiv, och avtar (grafen sjunker) när derivatan är negativ. Om en kontinuerlig funktion med en kontinuerlig derivata skall ha ett extremvärde (maximum eller minimum) i en inre punkt i sin definitionsmängd måste derivatan – om den existerar – följaktligen vara noll där. Punkter där derivatan är noll kallas stationära punkter, och mängden av de stationära punkterna och de punkter där derivatan inte existerar utgör mängden av de kritiska punkterna. De enda punkter i vilka en kontinuerlig funktion kan anta extremvärden är således de kritiska punkterna samt eventuella randpunkter. Därför används derivator flitigt vid systematiska optimeringsproblem – man finner genom ekvationslösning de punkter där derivatan är lika med noll. En stationär punkt kan antingen vara en maximipunkt, en minimipunkt eller en terrasspunkt; derivatans teckenväxling i punkten avgör dess karaktär: om derivatan exempelvis går från plus till minus är punkten en maximipunkt. Som ett alternativ till ett dylikt teckenstudium kan andraderivatan betraktas. Om denna är negativ (vilket är troligt, men inte nödvändigt, om derivatan växlar tecken från plus till minus) är punkten en maximipunkt. Om andraderivatan istället är positiv måste derivatan utföra teckenväxlingen minus till plus, och punkten måste vara en minimipunkt. I de fall andraderivatan är noll kan det såväl röra sig om en terrasspunkt som ett extremvärde. Nedan ges exempel på två funktioner som har stationära punkter i origo, och där andraderivatorna också är noll, men där den ena funktionen har en terrasspunkt medan den andra har ett extremum i form av en minimipunkt i origo.
Märk att förstaderivatan i origo har ett extremvärde i det första fallet och en terrasspunkt i det andra fallet.
Exempel
För att finna det största värdet som antages av funktionen definierad av f(x) = x3 − 2x2 + x − 3 för 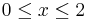 beräknar vi derivatan och bestämmer dess nollställen.
beräknar vi derivatan och bestämmer dess nollställen.
Eftersom andraderivatan är
så är
 och
och  .
.
Värdena i randpunkterna är f(0) = − 3 respektive f(2) = − 1.
Följaktligen har funktionen f en lokal maximipunkt för x = 1 / 3 och en lokal minimipunkt för x = 1. Respektive extremvärden är f(1 / 3) = − 77 / 27 och f(1) = − 3. Det minsta respektive största värde som antas i intervallet är alltså -3 (ändpunkt och lokal minimipunkt) och -1 (ändpunkt).
Fysik
Inom fysiken är derivator vanliga. Speciellt vanligt är derivator med hänseende på tiden, men även derivator med avseende på rumsvariabler förekommer. Inom klassisk mekanik ingår derivator av ett föremåls position nästan alltid i de problem som behandlas, vilket lett till att de fått egna namn, hastighet (förstaderivatan med avseende på tiden av positionen) och acceleration (andraderivatan av densamma). (Farten är absolutbeloppet av hastigheten.)
Reellvärda funktioner av flera variabler
En funktion av flera variabler kan deriveras med avseende på var och en av dessa; dessa partiella derivator anger då förändringhastigheten i respektive koordinataxels riktning. Vektorn som består av samtliga dessa partiella derivator kallas gradienten till funktionen och spelar en liknande roll för funktioner av flera variabler som den vanliga derivatan gör för funktioner av en variabel; till exempel kan lokala extrempunkter i det inre av definitionsmängden endast återfinnas där gradienten är lika med nollvektorn (eller inte existerar).
Vektorvärda funktioner
Funktioner av en variabel
För en vektorvärd funktion av en variabel
kan derivatan definieras som gränsvärdet
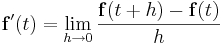 .
.
Eftersom
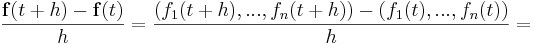
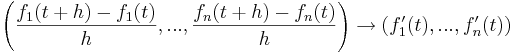 då
då 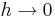
ser vi att en vektorvärd funktion faktiskt kan deriveras komponent för komponent; med andra ord återförs beräkningen av en vektoriell derivata på fallet med beräkningen av flera enkla derivator.
Exempel
Om vektorn 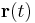 anger en partikels position i rummet vid tiden t så kommer första- respektive andraderivatan att ange partikelns hastighets- respektive accelerationsvektor vid tiden t.
anger en partikels position i rummet vid tiden t så kommer första- respektive andraderivatan att ange partikelns hastighets- respektive accelerationsvektor vid tiden t.
Funktioner av flera variabler
Derivatan av en vektorvärd funktion av två eller fler variabler är däremot mer komplicerad än derivering komponent-för-komponent. Följande funktion är ett exempel på en vektorvärd funktion av tre variabler:
Anledningen till att det är svårt att beräkna derivatan av en sådan funktion är att det blir problematiskt då man skall beräkna gränsvärdet av differenskvoten då 'h närmar sig noll'; för det första är h en vektor (inte ett tal som tidigare), och för det andra så finns det väldigt många sätt som en vektor kan närma sig origo. Den kan exempelvis röra sig i en spiral, röra sig längs en rät linje, röra sig längs en krokig linje och så vidare. Man måste täcka in alla dessa möjligheter då man beräknar derivatan av en vektorvärd funktion av flera variabler.
Komplexa funktioner
Vissa komplexvärda funktioner av en komplex variabel har derivata t.ex. analytiska funktioner.
Se även
- Analysens fundamentalsats
- Integral
- Logaritmisk derivering
- Partiell derivata
- Bruten derivata
- Differentialekvation
- Differentialgeometri
- Differentialtopologi
- Distributionsteori (vidareutveckling av begreppet derivata)
- Medelvärdessatsen (Lagranges medelvärdessats)