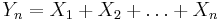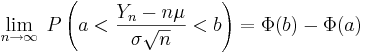Centrala gränsvärdessatsen

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Den centrala gränsvärdessatsen är en fundamental sats inom den matematiska statistiken. Satsen säger att om man adderar samman flera slumpmässiga variabler med en och samma sannolikhetsfördelning med ändlig varians, kommer summan gå mot en normalfördelning.

För den formella definitionen så låter vi X1, X2, ... vara en oändlig följd av oberoende och likafördelade stokastiska variabler med väntevärde μ och standardavvikelse σ > 0. Vidare så inför vi en stokastisk variabel för att beteckna summan av de första n stokastiska variablerna i följden, det vill säga

Y_n = X_1 + X_2 + \ldots + X_n

Då gäller att

\lim_{n \rightarrow \infty}\; P\left(a < \frac{Y_n - n\mu}{\sigma \sqrt{n}} < b\right) = \Phi(b) - \Phi(a)

där Φ(a) betecknar fördelningssfunktionen för en standardiserad normalfördelning.

Till exempel gäller att om man tar ett stort antal tärningar och slår dem så är summan av ögonen ungefär normalfördelad.

Hämtad från "https://sv.rilpedia.org/wiki/Centrala_gr%C3%A4nsv%C3%A4rdessatsen"
Personliga verktyg