Normalfördelning
Från Rilpedia
Normalfördelningen är inom matematiken (i synnerhet sannolikhetsteori och statistik) den absolut viktigaste fördelningen. En normalfördelad variabel antar ofta värden som ligger nära medelvärdet och mycket sällan värden som har stor avvikelse. Därför ser normalfördelningen ut som en kulle eller en klocka och internationellt används ofta beteckningen bell curve.
Normalfördelningen är statistikens absolut viktigaste fördelning. Detta hänger samman med ett matematiskt resultat som kallas centrala gränsvärdessatsen. Resultatet innebär att summan av ett stort antal oberoende slumpmässiga variabler är ungefär normalfördelad under vissa allmänna förutsättningar, oavsett vilken fördelning dessa variabler hade från början. Detta får till följd att normalfördelningen dyker upp på många ställen i naturen och samhället och mängder med skeenden kan med stor noggrannhet beskrivas av normalfördelningen. Inom naturvetenskap, sociologi, ekonomi med mera är det vanligt att man inte förstår hur en viss mekanism fungerar, men man kan teoretiskt motivera ett användande av normalfördelningar eftersom det ofta är sant att fenomen uppkommer genom många små, oberoende, slumpmässiga variationer.
Innehåll |
Exempel – singla slant
Om man singlar en slant 100 gånger och kallar summan för X så kommer X att vara binomialfördelad. Men eftersom varje slantsingling är oberoende av alla övriga kommer summan X att vara ungefär normalfördelad med väntevärde 50. Ofta är det mycket enklare att approximera en slumpmässig variabel med en normalfördelning än att beräkna sannolikheter exakt, och eftersom många slumpmässiga fenomen är summor av väldigt många små slumpmässiga tillskott fungerar det mycket bra. Historiskt sett var möjligheten att approximera stora binomialfördelningar det första tillämpningsområdet för normalfördelningen.
Definition
Normalfördelningen har täthetsfunktionen:
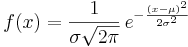 ,
,
där μ och σ är normalfördelningens karakteristiska konstanter: μ kallas väntevärdet, och σ kallas standardavvikelsen för fördelningen. Denna normalfördelning betecknas med 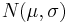 .
.
Normalfördelningens täthetsfunktion kan inte integreras med vanliga endimensionella metoder eftersom den inte har någon primitiv funktion som kan uttryckas analytiskt. Arean under kurvan kan emellertid med andra metoder visas vara 1, vilket den måste vara för att vara en riktig sannolikhetsfördelning.
En standardiserad normalfördelning har μ = 0 och σ = 1.
Fördelningsfunktionen för en standardiserad normalfördelning brukar betecknas med 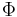 och sambandet mellan fördelningsfunktion och täthetsfunktion säger att:
och sambandet mellan fördelningsfunktion och täthetsfunktion säger att:
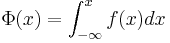 .
.
Fördelningsfunktionen anger sannolikheten att en normalfördelad variablel Y är mindre än eller lika med ett visst tal x:
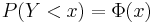 .
.
Sannolikheten att en normalfördelad variabel hamnar i ett interval [a,b] är:
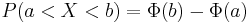 .
.
Egenskaper
Följande egenskaper gäller för normalfördelningar:
Fördelningsfunktion
Fördelningsfunktionen för en godtycklig normalfördelad variabel 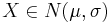 kan lätt erhållas från fördelningsfunktionen för en standard-normalfördelad variabel:
kan lätt erhållas från fördelningsfunktionen för en standard-normalfördelad variabel:
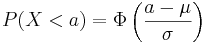 .
.
Denna egenskap gör att tabeller för normalfördelningar bara redovisar fördelningsfunktionen 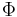 , eftersom alla andra normalfördelningar på detta sätt kan översättas till en med väntevärdet 0 och standardavvikelse 1.
, eftersom alla andra normalfördelningar på detta sätt kan översättas till en med väntevärdet 0 och standardavvikelse 1.
Symmetri
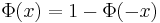 .
.
Denna symmetri gör att alla tabeller bara redovisar 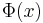 för positiva tal x.
för positiva tal x.
Linjär förändring
Om 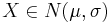 och
och 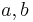 är konstanter så gäller att den linjära formen
är konstanter så gäller att den linjära formen
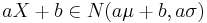 ,
,
det vill säga väntevärdet förändras på samma linjära sätt och standardavvikelsen ökar med faktorn a.
Summa av två oberoende normalfördelade variabler
Om 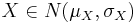 och
och 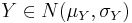 är oberoende så gäller att deras summa
är oberoende så gäller att deras summa
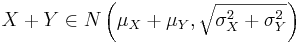 .
.
Differenser av oberoende normalfördelade variabler fungerar analogt.






