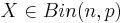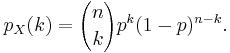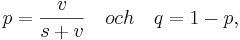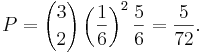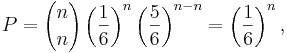Binomialfördelning

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Galtons bräda ger en normalfördelning

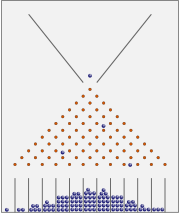
En binomialfördelning är en diskret fördelning (begrepp inom sannolikhetsteori och matematisk statistik) som hanterar upprepade (diskreta) försök med fix sannolikhet.

Om en stokastisk variabel X är binomialfördelad, med n=antalet försök och p=sannolikheten att lyckas i varje försök, skriver man :

$X \in Bin(n,p)$

X har sannolikhetsfunktionen

$p_X(k) = {n \choose k} p^k (1-p)^{n-k}.$

Där p är sannolikheten att händelsen skall inträffa och 1 - p = q således sannolikheten att händelsen inte skall inträffa. Som synes dyker binomialkoefficienterna upp i fördelningen.

Binomialfördelningen kan under vissa omständigheter approximeras med andra fördelningar. Tumreglerna är att om $p < 0,1$ kan fördelningen approximeras med poissonfördelningen Po(np), eller om $n p (1 - p) > 10$ med normalfördelningen N( $n p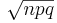$ , $\sqrt{npq}$ ).

Exempel: statistikerns favoritexempel är urnmodeller som bygger på urnor med svarta och vita kulor. Sannolikheten att dra en vit kula vid en slumpmässig dragning är p. Sannolikheten att man drar exakt k stycken vita kulor vid n försök om man har s stycken svarta och v st vita kulor i en urna och lägger tillbaka kulorna mellan dragningarna (dragning med återläggning) ges då av sannolikhetsfunktionen ovan med

$p = {v \over {s+v}} \quad och \quad q = 1 - p,$

där p och q ges genom den klassiska sannolikhetsdefinitionen.

Exempel 2: Om man kastar en tärning tre gånger, och tärningen är välgjord, så att sannolikheten att få en sexa är 1/6, blir sannolikheten att få sexa två gånger

$P = {3 \choose 2} \left( {1 \over 6} \right)^2 {5 \over 6} = {5 \over 72}.$

Exempel 3: På samma vis kan man räkna ut sannolikheten för att vid n st kast få siffran sex n gånger:

$P = {n \choose n} \left( {1 \over 6} \right)^n \left( {5 \over 6} \right)^{n-n} = \left( {1 \over 6} \right)^n,$

vilket vi ju kunde misstänka eftersom det rör sig om n st oberoende utfall med vardera sannolikheten (1/6).

Se även

Binomialsatsen

Binomialfördelning

Från Rilpedia

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk