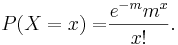Poissonfördelning

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

P som funktion av heltalen x för m=1, 4 och 10.

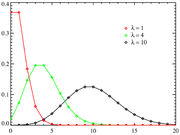
Poissonfördelning är en diskret sannolikhetsfördelning som används för att beskriva företeelser som inträffar oberoende av varandra. Den approximerar binomialfördelningen om $n$ är stort och $p$ är litet (tumregel: om $p < 0,1$ kan den aktuella binomialfördelningen approximeras med poissonfördelningen Po(m) där $m = n p$ ). Sannolikhetsfunktionen är

${P(X=x) =} {{e^{-m} m^x} \over x!}.$

Poissonfördelningen har egenskapen att väntevärdet och variansen båda är $m$ .

Poissonprocess

Poissonprocess är en heltalsvärd stokastisk process i kontinuerlig tid som används för att beskriva slumpmässiga händelser som sker med en viss intensitet. Processen används i tillämpningar när man ska beskriva till exempel en kö, såsom kunder vid ett bankkontor. Om intensiteten är konstant talar man om en homogen Poissonprocess, i annat fall är processen inhomogen. Det gäller för en Poissonprocess X(t), 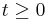$t \geq 0$ med intensitetsfunktion $λ(t)$ att:

X(t) är heltalsvärd och ökande. Dessutom är X(0) = 0
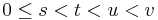
X(t) har oberoende ökningar. Det innebär att X(t) - X(s) och X(v) - X(u) är oberoende för varje val av $0 \leq s < t < u < v$
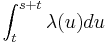
$X (s + t) - X (t)$ är Poissonfördelad med parameter $\int_{t}^{s+t} \lambda(u) du$

Dessutom, om λ är konstant är processen stationär, och händelseavstånden är oberoende och exponentialfördelade.

Poissonprocessen kan generaliseras till en mer allmän delmängd av 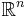$\mathbb{R}^n$ . Poissonprocessen är ett exempel på en förnyelseprocess.

Poissonfördelning

Från Rilpedia

Poissonprocess

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk