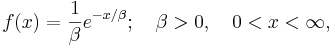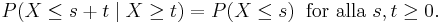Exponentialfördelning
Från Rilpedia
Exponentialfördelning, inom matematisk statistik är en beskrivande modell på tiderna mellan händelser i en Poissonprocess. Exponentialfördelningen är kontinuerlig sannolikhetsfördelning med täthetsfunktionen
där β > 0 är en parameter i fördelningen. Väntevärdet E(X) och variansen V(X) ges av
- E(X) = β,
- V(X) = β2.
Exponentialfördelningen är alltså ett specialfall av gammafördelningen, där Exp(β) = Γ(1,β). Detta innebär bl a att summan av två oberoende exponentialfördelade stokastiska variabler med parameter β har fördelningen Γ(2,β).
Exponentialfördelningen används bl a för att modellera homogena Poisson-processer, vilket är en heltalsvärd stokastisk process där tillståndet förändras med konstant sannolikhet per tidsenhet λ. Avstånden mellan tillståndsförändringarna är då exponentialfördelade med väntevärde λ. Därför är integralen från 0 till T över f sannolikheten att minst en tillståndsförändring skett vid tiden T.
Exponentialfördelningen kan ses som en kontinuerlig version av den geometriska fördelningen, vilken beskriver antalet försök som behövs för att en diskret process skall byta tillstånd. I motsats till detta beskriver exponentialfördelningen den tid det tar för en kontinuerlig process att byta tillstånd.
Exempel på variabler som är approximativt exponentialfördelade är:
- tiden det tar tills du råkar ut för nästa bilolycka
- tiden det tar tills du får nästa telefonsamtal
- avståndet mellan mutationer på en DNA-sträng
En viktig egenskap hos exponentialfördelningen är att den "saknar minne". Detta innebär att om en slumpvariabel X är exponentialfördelad så är dess betingade sannolikhet
Med andra ord, chansen att tillståndet kommer att förändras inom de nästa s sekunderna påverkas inte av den tid som redan har förflutit.