Stokastisk process

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Inom sannolikhetsteorin är en stokastisk process ett matematiskt objekt som används för att beskriva slumpmässiga (stokastiska) förändringar. Slumpmässigheten gör att det inte är tillräckligt att exempelvis betrakta ett system av differentialekvationer. Detta räcker däremot när man har full kunskap om utgångsläget och processen är deterministisk, det vill säga senare "händelser" fullständigt bestäms av tidigare.

Till exempel kan astronomer utan vidare räkna ut i vilka stjärnbilder en jordisk amatörastronom kan hitta de synliga planeterna vid vårdagjämningen år 2345, därför att planeternas rörelser under ett par hundra år kan analyseras som en deterministisk process. Däremot är det fundamentalt omöjligt att avgöra precis var ett tiotal olika gasmolekyler som stängts in i ett litet utrymme befinner sig efter femton minuter, eftersom så mycket av deras rörelse påverkas av ren slump. I det senare fallet kan man däremot modellera systemet som en stokastisk process, och därmed ange sannolikheten för att till exempel alla tio molekylerna befinner sig i övre halvan av utrymmet vid slutet av kvarten.

Formell definition

En reellvärd stokastisk process X är en samling 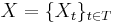X = \{X_t\}_{t \in T} av stokastiska variabler 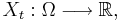X_t : \Omega \longrightarrow \mathbb{R}, som är definierade på samma sannolikhetsrum 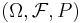(\Omega, \mathcal{F}, P). Om index-mängden T är diskret, säger man att X är en stokastisk process i diskret tid, och om index-mängden är kontinuerlig säger man att X är en stokastisk process i kontinuerlig tid.

Sannolikhetsfördelningen för en stokastisk variabel är ett sannolikhetsmått μt på Borel sigma-algebran på mängden av de reella talen 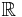\mathbb{R}:

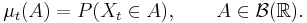
\mu_t(A) = P(X_t \in A), \qquad A \in \mathcal{B}(\mathbb{R}).

De ändligt-dimensionella fördelningarna för en stokastisk process är mängden 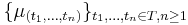\{\mu_{(t_1,\dots,t_n)}\}_{t_1,\dots,t_n \in T, n\geq1} av alla tänkbara flerdimensionella sannolikhetsfördelningar associerade med den stokastiska processen:

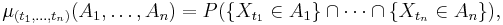
\mu_{(t_1,\dots,t_n)}(A_1,\dots,A_n) = P(\{X_{t_1} \in A_1\} \cap \cdots \cap \{X_{t_n} \in A_n\}),

där index 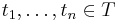t_1,\dots,t_n \in T och mängderna 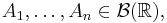A_1,\dots,A_n \in \mathcal{B}(\mathbb{R}), för varje val av heltalet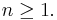 n\geq 1.

Associerade med en stokastisk process är dess väntevärdesfunktion

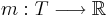
m : T \longrightarrow \mathbb{R}

och dess kovariansfunktion

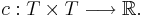
c : T \times T \longrightarrow \mathbb{R}.

Dessa är definierade av följande integraler med avseende på sannolikhetsmåttet P.

m(t) = E[X_t] = \int_{\Omega} X_t(\omega)\, dP(\omega)

och

c(s,t) = E[XsXt] − E[Xs]E[Xt],

där väntevärdet E[XsXt] beräknas på produktrummet 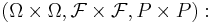(\Omega\times\Omega,\mathcal{F}\times\mathcal{F},P\times P):

E[X_s X_t] = \int_{\Omega\times\Omega} X_s(\omega) X_t(\eta) \, d(P\times P)(\omega,\eta).

Om det råkar vara så att de ändligt-dimensionella fördelningarna för den stokastiska processen X är absolutkontinuerliga med avseende på Lebesgue-måttet, så kan ovanstående väntevärden skrivas som

E[X_t] = \int_{-\infty}^{\infty} x f_{X_t}(x)\,dx

och

E[X_s X_t] = \int_{-\infty}^\infty \int_{-\infty}^\infty x y f_{(X_s,X_t)}(x,y) \, dx \, dy,

där funktionen 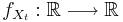f_{X_t} : \mathbb{R} \longrightarrow \mathbb{R} är Radon-Nikodym derivatan av sannolikhetsfördelningen för den stokastiska variabeln Xt med avseende på Lebesgue-måttet på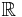 \mathbb{R}

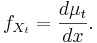
f_{X_t} = \frac{d \mu_t}{dx}.

Denna derivata kallas inom sannolikhetsteori och statistik för den stokastiska variabelns täthetsfunktion. På motsvarande sätt är funktionen 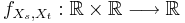f_{X_s,X_t} : \mathbb{R}\times\mathbb{R} \longrightarrow \mathbb{R} Radon-Nikodym derivatan

f_{X_s,X_t} = \frac{\mu_{s,t}}{dx dy}

av sannolikhetsfördelningen för den två-dimensionella stokastiska variabeln (Xs,Xt) med avseende på Lebesgue-måttet i planet 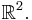\mathbb{R}^2.



Stokastiska processer är vanligt förekommande inom såväl teknik som ekonomisk och finansiell teori.

Hämtad från "https://sv.rilpedia.org/wiki/Stokastisk_process"
Personliga verktyg