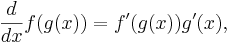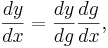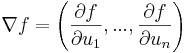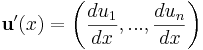Kedjeregeln
Från Rilpedia
Kedjeregeln, regel som talar om hur man deriverar sammansatta funktioner.
Om
- y = f(u) och u = g(x), så att y = f(g(x)),
anger kedjeregeln att
eller med Leibniz notation
där det är den senare notationen som har gett upphov till namnet kedjeregeln.
I flervariabelanalys fungerar kedjeregeln på ett liknande sätt.
Om
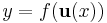 och
och 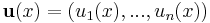
så är
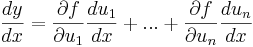 .
.
Eftersom gradienten
och derivatan av den inre funktionen u är
inser vi att derivatan 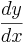 kan skrivas som en skalärprodukt enligt
kan skrivas som en skalärprodukt enligt
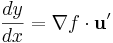 .
.
Detta bekräftar att gradienten spelar samma roll inom flervariabelanalysen som den enkla derivatan inom envariabelanalysen.
Not: Normalt görs ingen skillnad i notationen mellan variablerna un och funktionerna gn(x), utan låter dessa betecknas med samma bokstav. För tydlighets skull har dock dessa skilts åt.