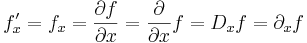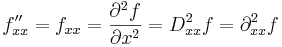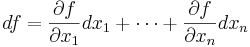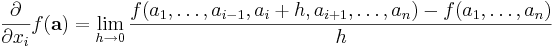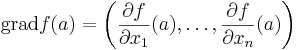Partiell derivata

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Innehåll

Introduktion, enkla exempel

En partiell derivata till den reellvärda funktionen f(x1,x2, .. , xn) är en funktion 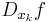D_{x_k} f (där k är ett heltal mellan 1 och n, inklusive gränserna) som beskriver hur snabbt f växer med avseende på variabeln xk.

När man deriverar en funktion av flera variabler betraktar man alla variabler utom den som ska deriveras med avseende på som konstanter.

Exempel

f = x2y

så är

Dx f = 2yx

och

Dy f = x2.

Högre derivator bildas på motsvarande sätt som för de ordinära derivatorna:

Fortsättning på exemplet
Dxx f = 2y (Låt y vara konstant; derivera funktionen som nu bara beror på x två gånger)
Dyy f = 0 (Låt x vara konstant; derivera funktionen som nu bara beror på y två gånger)
Dxy f = 2x

Den sista bör uppmärksammas. Den anger att man först betraktar y som en konstant och deriverar med avseende på x. Resultatet kan betraktas som en ny funktion av två variabler. Denna nya funktion kan sedan deriveras med avseende på y.

Notera också att Dxy f = Dyx f om f är deriverbar tillräckligt många gånger.


Beteckningar

Ett flertal olika beteckningar används för partiella derivator. Vi har bland annat:

f^\prime_x = f_x = {\partial f \over \partial x} = {\partial \over \partial x}f = D_x f = \partial_x f

och för högre derivator

f^{\prime\prime}_{xx} = f_{xx}= {\partial^2 f \over \partial x^2} = D^2_{xx} f = \partial^2_{xx} f

Differential

Se även artikeln differential

Differentialen av funktionen f(x1,x2, .. , xn) definieras som

df = {\partial f \over \partial x_1}dx_1 + \cdots + {\partial f \over \partial x_n}dx_n

Detta kan tolkas som att om xi ändras ytterst lite (med storleken dxi), så ändras f med ungefär df.

Jämför med specialfallet då funktionen bara beror på en variabel.

Exempel

Volymen av en kon med höjden h och basradien r ges av 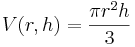V(r,h)=\frac{\pi r^2 h}{3}.

Då blir 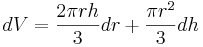dV = \frac{2\pi r h}{3}dr + \frac{\pi r^2}{3}dh

Formella egenskaper

Även de partiella derivatorna definieras genom gränsvärden.

Låt U vara en öppen delmängd i Rn där den reellvärda funktionen f är definierad.

Den partiella derivatan av f i punkten a=(a1,...,an)∈U med avseende på variabeln xi som

\frac{ \partial }{\partial x_i }f(\mathbf{a}) = \lim_{h \rightarrow 0}{ f(a_1, \dots , a_{i-1}, a_i+h, a_{i+1}, \dots ,a_n) - f(a_1, \dots ,a_n) \over h }

En skillnad mot ordinära derivator är att även om alla partiella derivator ∂f/∂xi(a) existerar i en given punkt a, så behöver inte funktionen vara kontinuerlig där. Om däremot samtliga derivator existerar i en omgivning av a och är kontinuerliga där, så är f differentierbar där, och differentialen är då kontinuerlig. Då säges f tillhöra mängden C1 (eller vara en C1-funktion)

De partiella derivatorna ∂f/∂xi kan betraktas som nya funktioner definierade på U. Dessa kan åter deriveras partiellt. Om samtliga blandade derivator existerar och är kontinuerliga, så kallas f för en C2-funktion. I detta fall kan de partiella derivatorna byta ordning:

\frac{\partial^2f}{\partial x_i\, \partial x_j} = \frac{\partial^2f} {\partial x_j\, \partial x_i}

Vektorn bestående av alla partiella derivator av f i en given punkt a kallas gradienten av f i punkten a:

\operatorname{grad}f(a) = \left( \frac{\partial f}{\partial x_1}(a), \dots , \frac{\partial f}{\partial x_n}(a) \right)

Om f är en C1-funktion, så har grad f(a) en geometrisk betydelse: vektorn pekar åt det håll i vilket f växer snabbast.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Partiell_derivata"
Personliga verktyg