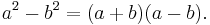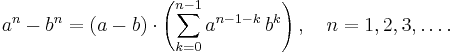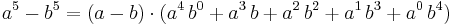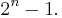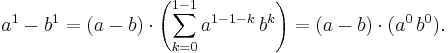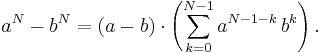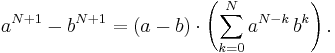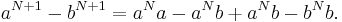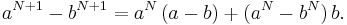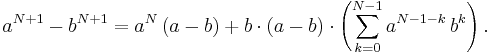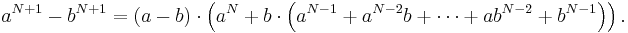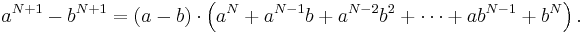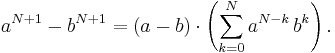Från Rilpedia

Inom matematik är konjugatregeln ett ofta använt resultat då man vill skriva en differens som en produkt. Om a och b är två tal så är

Konjugatregeln gäller även för andra matematiska objekt än tal. Objekten a och b måste då kommutera.

Innehåll 1 Den allmänna konjugatregeln 1.1 Exempel 1.2 Tillämpning inom talteori 1.3 Bevis av den allmänna konjugatregeln 2 Se även

Den allmänna konjugatregeln

Om man ersätter exponenten 2 med ett annat positivt heltal får man vad som kallas den allmänna konjugatregeln:

Exempel

Tillämpning inom talteori

Låt a, b och n beteckna positiva heltal. Den allmänna konjugatregeln visar att ett tal på formen 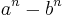bara kan vara ett primtal om differensen mellan a och b är ett. Om man är intresserad av att hitta primtal på denna form är det därför tillräckligt att inskränka letandet till tal av typen 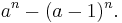Speciellt ger valet a = 2 det som kallas Mersennetal:

För vissa värden på det positiva heltalet n är ett primtal (Mersenneprimtal); för sådana värden måste följande tal vara ett primtal enligt konjugatregeln.

.

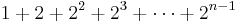Bevis av den allmänna konjugatregeln

Vi bevisar den allmänna konjugatregeln med hjälp av matematisk induktion med avseende på det positiva heltalet n:

• Först visar vi att regeln är sann då n=1.
• Sedan antar vi att regeln är sann då n=N, där N är ett positivt heltal.
• Sedan visar vi att regeln är sann för nästa positiva heltal n=N+1.
• Slutligen åkallar vi principen för matematisk induktion som låter oss säga att regeln är sann för alla positiva heltal n.

Då det positiva heltalet n=1, säger den allmänna konjugatregeln att följande samband råder:

Eftersom a^1 = a och b^1 = b och a^0 = 1 och b^0 = 1, så säger den allmänna konjugatregeln i detta fall att 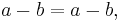vilket vi vet är sant. Den allmänna konjugatregeln är därför sann för det positiva heltalet n=1.

Vi antar nu att den allmänna konjugatregeln är sann för det positiva heltalet n=N, det vill säga:

Med utgångspunkt från detta antagande skall vi visa att regeln är sann för nästa positiva heltal; Vi skall därför bevisa att:

För att göra detta använder vi ett matematiskt knep:

Vi gör ingenting, men vi gör det på ett smart sätt!

I detta fall handlar det om att skriva om differensen a^{N + 1} − b^{N + 1} på ett sätt som gör att vi kan använda det vi vet om differensen a^N − b^N;

Vi slår samman de termer som innehåller faktorn a^N och vi slår även samman de termer som innehåller faktorn b:

Nu ersätter vi differensen a^N − b^N med det uttryck som vi har antagit vara sant:

Sedan bryter vi ut den gemensamma faktorn och skriver ut i detalj det som blir kvar:

Om vi multiplicerar in faktorn b i summan ovan ser vi att:

Med hjälp av summa-symbolen kan vi skriva vårt resultat på en form som visar att vi har uppnått det vi ville visa, nämligen att:

Vi har härmed lyckats visa att om den allmänna konjugatregeln är sann för det positiva heltalet n=N, så är den även sann för nästa positiva heltal n=N+1.

Enligt principen för matematisk induktion är den allmänna konjugatregeln sann för alla positiva heltal n.

Se även

• Konjugat (Algebra)
• Kvadreringsreglerna